题目
https://leetcode.com/problems/bulb-switcher/description/
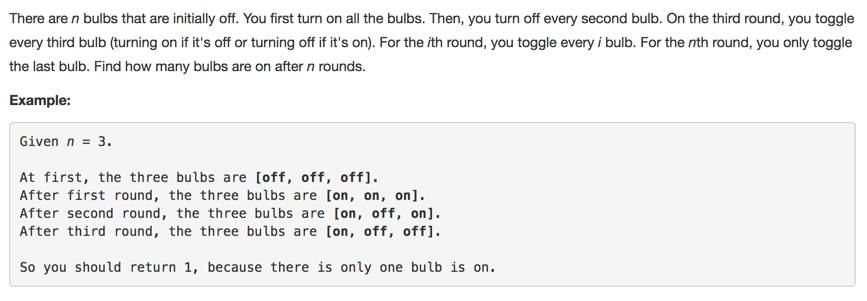
想法
注意题意是toggle!
对一个数因式分解,如果不同的因式数量是奇数,则on;如果偶数,则off
1 : 1 on
2 : 1, 2 off
3 : 1, 3 off
4 : 1, 2, 4 on
…
8 : 1, 2, 4, 8 off
找到一个数的不同因数
Number of Factors of an Integer
http://www.cut-the-knot.org/blue/NumberOfFactors.shtml
$n = a^pb^q…c^r$
where a, b, c is prime
8: 2^3 3个+1个(1)
4: 2^2 2个+1
3: 3^1 1+1个
9: 1, 3, 9 — 3^2 2+1个
12: 1, 2, 3, 4, 6, 12 — 2^2 3^1 (2+1)(1+1)
所以最终得到:(p+1)(q+1)…(r+1)个,其中包括了其本身和1
转化为找到其素因数
先找出素数表,再除去就可以了
!!想错了,这只找出了最后一个灯的亮灭
看了高票的答案,自己想对了部分,但是关键的一点没有想到,就是只有完全平方数最后才会保持亮着!!!
一个答案
A bulb ends up on iff it is switched an odd number of times.
Call them bulb 1 to bulb n. Bulb i is switched in round d if and only if d divides i. So bulb i ends up on if and only if it has an odd number of divisors.
Divisors come in pairs, like i=12 has divisors 1 and 12, 2 and 6, and 3 and 4. Except when i is a square, like 36 has divisors 1 and 36, 2 and 18, 3 and 12, 4 and 9, and double divisor 6. So bulb i ends up on if and only if i is a square.
So just count the square numbers.
Let R = int(sqrt(n)). That’s the root of the largest square in the range [1,n]. And 1 is the smallest root. So you have the roots from 1 to R, that’s R roots. Which correspond to the R squares. So int(sqrt(n)) is the answer. (C++ does the conversion to int automatically, because of the specified return type).
优秀!
回顾
这道题,自己最后还是没有想到,一道算是找规律的题吧,虽然自己发现了些道理,但是还是没有进一步的发现,加油吧!