Combination Sum III

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/combination-sum-iii/description/

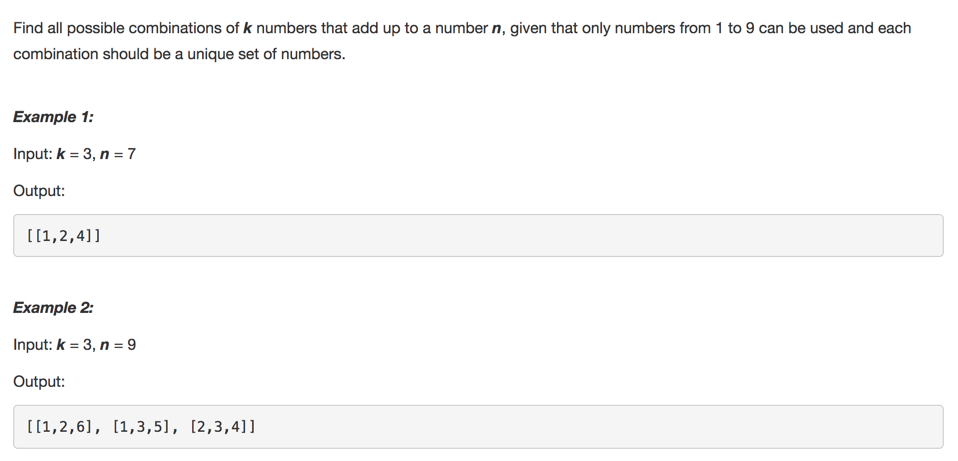
想法

首先是unique的，其次所有的数的数量是定死的

遍历应该是不行的，那样，简单的递归应该也不可以，

用DP也不现实，会算好多没用的

这样想，先分配：
1, 2, …, k
然后减去之后剩下的，问题变成了剩下的里边选几个再加
不好操作

先分配：1, 1, 1, …, 1
然后变成剩下的用0-8来分
没有区别。。。

答案

没有想出来，其它人的想法：

backtracking!!!这应该是一个比较经典的backtracking的题目，只是自己不是很会backtracking罢了，趁机学习一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int>> ans;
    void combination(vector<int> &vec, int current_sum, int start, int k, int n) {
        if (k == 0)
            return;
        for (int i = start; i <= 9; i++) {
            if (current_sum + i == n && k == 1) {
                vec.push_back(i);
                ans.push_back(vec);
                vec.pop_back();
                return;
            } else if (current_sum + i < n) {
                vec.push_back(i);
                combination(vec, current_sum + i, i + 1, k - 1, n);
                vec.pop_back();
            } else {
                return;
            }
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        vector<int> vec;
        combination(vec, 0, 1, k, n);
        return ans;
    }
};

回顾

其实自己一开始是这样想的，但是觉得这种递归是很低效的。但其实还是没有理解回溯的思想，没有条件反射地想到。

回溯核心在于维护一个序列，当不满足条件时便退回，这个序列保证了不会做多余的工作，不像简单的递归一样！