221. Maximal Square

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/maximal-square/description/

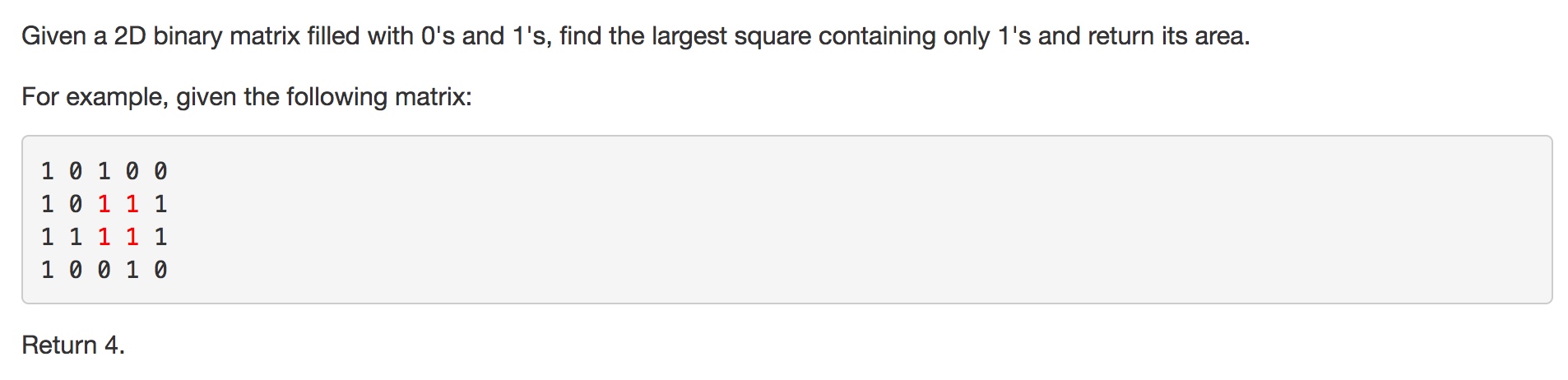
想法

直觉告诉我，这是用DP做的
但如果很单纯地算各个大小的块的话，空间太浪费了

没有想法，看别人的解答

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution(object):
    def maximalSquare(self, matrix):
        """
        :type matrix: List[List[str]]
        :rtype: int
        """
        if not matrix:
            return 0
        max_size = [[0 for i in range(len(matrix[0]))] for j in range(len(matrix))]
        for i in range(len(matrix)):
            max_size[i][0] = int(matrix[i][0])
            
        for i in range(len(matrix[0])):
            max_size[0][i] = int(matrix[0][i])
            
        for i in range(1, len(matrix)):
            for j in range(1, len(matrix[0])):
                if int(matrix[i][j]) == 0:
                    max_size[i][j] = 0
                else:
                    max_size[i][j] = min(max_size[i - 1][j - 1], max_size[i][j - 1], max_size[i - 1][j]) + 1
        
        return max([max(l) for l in max_size]) ** 2

根据别人的想法写出来的

回顾

其实DP的确是运用在此处的，但是自己没有找到所谓的state equation，关系等式

而在这个题目中，关键的关系等式就是：

1
max_size[i][j] = min(max_size[i - 1][j], max_size[i][j - 1], max_size[i - 1][j - 1]) + 1

自己最开始想的是计算出每一点是最大的，认为会浪费太多的时间，便是其实并不知道每个点最终能够有多大的空间，而是要讨论其中一个（比如右下角）最后能张成多大的空间就可以了，这是关键！