42. Trapping Rain Water

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/trapping-rain-water/description/

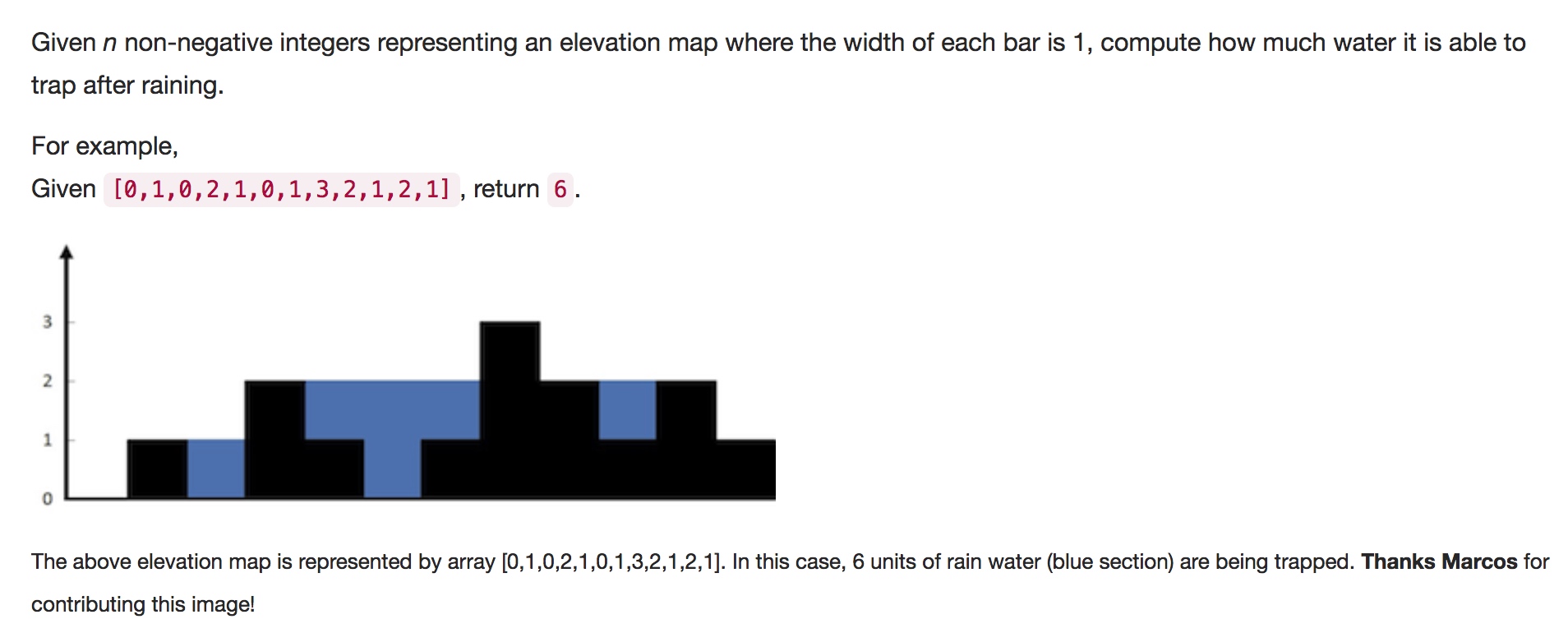
想法

每个块，直到遇到下一个>=它的块，则存储确定…

每个块都假定能盛满，直到最后遇不到>=自己的块

从左往右扫一遍，记录valid和如果valid所装的容量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    struct Bar {
        int s;
        bool v;
        Bar() : s(0), v(false) {}
    };
    int trap(vector<int>& height) {
        vector<Bar> content(height.size());
        int s = 0;
        for (int i = 1; i < height.size(); i++) {
            for (int j = s; j < i && content[j].v == false; j++) {
                if (height[j] <= height[i]) {
                    content[j].v = true;
                    if (j == s)
                        s = i;
                } else {
                    content[j].s += height[j] - height[i];
                }
            }
        }
        int res = 0;
        int maxHeight = 0;
        for (int i = 0; i < content.size(); i++) {
            if (height[i] >= maxHeight && content[i].v) {
                maxHeight = height[i];
                res += content[i].s;
            }
        }
        return res;
    }
};

错误！！！
都没有考虑最基础的情况： [4, 2, 3]
自己的答案在这个情况下，认为4没有找到>=它的，所以invalid，也就没有后边的容量了

看了discussion，发现自己还是没有想到简单解决问题的关键：

Here is my idea: instead of calculating area by height*width, we can think it in a cumulative way. In other words, sum water amount of each bin(width=1).
Search from left to right and maintain a max height of left and right separately, which is like a one-side wall of partial container. Fix the higher one and flow water from the lower part. For example, if current height of left is lower, we fill water in the left bin. Until left meets right, we filled the whole container.

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int trap(vector<int>& height) {
        int maxLeft = 0;
        int maxRight = 0;
        int res = 0;
        int l = 0, r = height.size() - 1;
        while (l <= r) {
            if (height[l] <= height[r]) {
                if (height[l] >= maxLeft)
                    maxLeft = height[l];
                else
                    res += maxLeft - height[l];
                l++;
            } else {
                if (height[r] >= maxRight) {
                    maxRight = height[r];
                } else {
                    res += maxRight - height[r];
                }
                r--;
            }
        }
        return res;
    }
};

回顾

记录左右的最高值，只要比本侧的最高值低且比另一侧低，就肯定会被填满…

抓住问题的管家哇，分析关系！