Binary Search Tree 相关算法总结

这些基础总是学了，长时间不看又忘了，这次写一篇文章记录下来，供日后回顾复习。

---

基本性质

首先是一个二叉树，数据结构：

struct Node {
    int val;
    Node *left;
    Node *right;
};

作为搜索树的性质：左子树节点的值 <= 根节点的值 <= 右子树节点的值

遍历

中序遍历

对于二叉搜索树来说，中序遍历输出的就是从小到大的顺序。

inorder_walk(node):
    if node != nil
        inorder_walk(node.left)
        print node.val
        inorder_walk(node.right)

CPP实现：

void inorder_walk(Node * node) {
    if (node) {
        inorder_walk(node->left);
        cout << node->val << endl;
        inorder_walk(node->right);
    }
}

遍历的话，用递归的方式都很直观，但如果用迭代的方式，就稍微有些麻烦，借助栈可以记录之前遍历的状态，进而实现中序遍历：

inorder_walk(node):
    stack s
    root = node
    while !(s.empty() and root == nil) # 结束的状态需要两个条件！！！
        while root != nil
            s.push(root) # 先把所有的左节点进栈
            root = root.left
        
        root = s.top()
        print root.val
        s.pop()
        root = root.right

CPP的实现，这里LeetCode上的题94. Binary Tree Inorder Traversal正好可以用以验证，就直接复制自己的答案了：

vector<int> inorderTraversal(TreeNode* root) {
    stack<TreeNode *> s;
    vector<int> res;
    while (!(root == NULL && s.empty())) {
        while (root != NULL) {
            s.push(root);
            root = root->left;
        }
        root = s.top();
        res.push_back(root->val);
        s.pop();
        root = root->right;
    }
    return res;
}

前序遍历

先输出根的值，再输出左右的值。

preorder_walk(node):
    if node != nil
        print node.val
        preorder_walk(node.left)
        preorder_walk(node.right)

非递归可以用中序同样的方式来遍历，但是输出的时机不同应该就可以了。
144. Binary Tree Preorder Traversal

vector<int> preorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode *> s;
    while (!(root == NULL && s.empty())) {
        while (root != NULL) {
            res.push_back(root->val);
            s.push(root);
            root = root->left;
        }
        
        root = s.top();
        root = root->right;
        s.pop();
    }
    return res;
}

其实在遍历过程中时使用迭代时，同样有递归的思想在里边，将root调整到右节点上，便相当于把右子树当做一个新的二叉树来进行处理，这种思想在构造迭代的时候还是很有用的。

后序遍历

先输出孩子的值，再输出根的值。

postorder_walk(node):
    if node != nil
        postorder_walk(node.left)
        postorder_walk(node.right)
        print node.val

非递归的算法自己还的确没有想出来，不过看了LeetCode上的Discussion：Preorder, Inorder, and Postorder Iteratively Summarization. 哇，的确没有注意到这一个性质。

前序遍历的时候，最先输出的是从根节点一直到最左叶节点的一列；而后序遍历的时候，最后输出的，就是从最右叶节点到根节点的最后一列！如图所示：

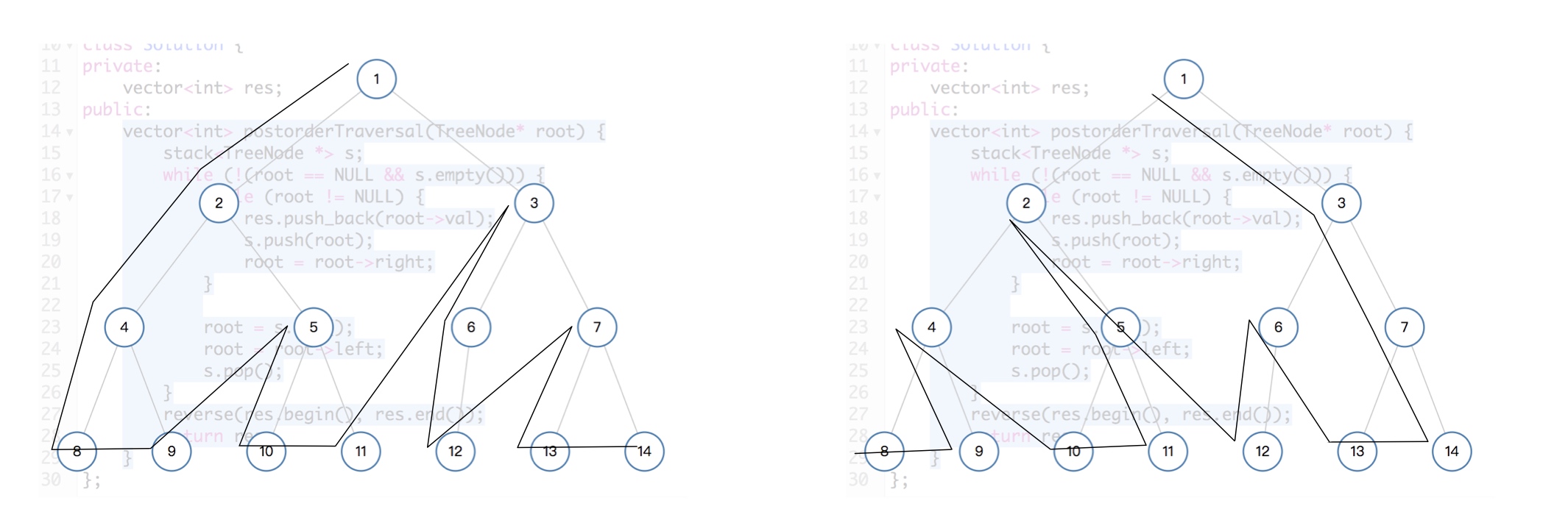
左为前序遍历，右为后序遍历，可以清楚的看到这个遍历顺序的性质！！

这样在实现的时候，便可以参照前序遍历，相反对称操作下，可以得到后序遍历的结果！

CPP的实现：LeetCode 145. Binary Tree Postorder Traversal

vector<int> postorderTraversal(TreeNode* root) {
    stack<TreeNode *> s;
    while (!(root == NULL && s.empty())) {
        while (root != NULL) {
            res.push_back(root->val);
            s.push(root);
            root = root->right;
        }
        
        root = s.top();
        root = root->left;
        s.pop();
    }
    reverse(res.begin(), res.end());
    return res;
}

层级遍历

层级遍历的话，用一个队列来存储每个节点，当出队列时，把它的两个孩子入队列，直到队列为空。

levelorder_walk(root):
    if root == nil
        return
    queue q
    q.push(root)
    while q not empty
        node = q.front()
        print node.val
        q.pop()
        if node.left != nil
            q.push(node.left)
        if node.right != nil
            q.push(node.right)

CPP实现，LeetCode 102. Binary Tree Level Order Traversal
由于这道题要求区分每一层，所以用了两个不同的queue来记录每一层的节点，不过思想大致相同。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q1, q2;
        vector<vector<int>> res;
        if (root == NULL)
            return res;
        q1.push(root);
        vector<int> vals;
        while (!q1.empty()) {
            TreeNode* node = q1.front();
            q1.pop();
            vals.push_back(node->val);
            if (node->left)
                q2.push(node->left);
            if (node->right)
                q2.push(node->right);
            if (q1.empty()) {
                res.push_back(vals);
                if (!q2.empty()) {
                    vals.clear();
                    while(!q2.empty()) {
                        q1.push(q2.front());
                        q2.pop();
                    }
                }
            }
        }
        return res;
    }
};

深度遍历

深度遍历是最普通最直观的二叉树遍历，其一般都结合具体的需求使用，比如查找，确定高度等等。

查找

利用搜索树的性质，查找很直观：

search(root, key):
    if root == nil or key == root.val
        return root
    if key < root.val
        return search(root.left, key)
    else
        return search(root.right, key)

非递归的方式也很直观，因为上述的递归是尾递归：

search(root, key):
    while root != nil and key != root.val
        if key < root.val
            root = root.left
        else
            root = root.right
    return root

插入

二叉搜索树的插入只是在查找的基础上做一点微小的改动。因为查找已经找到了对应的位置，只要在找到的位置上放上新的值即可。

删除

BST的删除需要考虑几个情况：

1. 叶节点：直接删掉
2. 只有一个子节点：删掉，子节点顶替删除的节点的位置
3. 有两个孩子：删掉，用左子树的最大节点或右子树的最小节点顶替

描述起来很清楚，但是真正写起来，需要考虑具体的一些细节，比如根节点的情况，比如如何去做“顶替”这一操作

delete(root, key):
    if root == nil
        return nil
    if key < root.val
        root = delete(root.left, key)
    else if key > root.val
        root = delete(root.right, key)
    else # find node to delete
        # 以下的两种情况涵盖了都是nil的情况，这是实践中的一点小小的hack吧
        if root.left == nil
            return root.right
        if root.right == nil
            return root.left
        right_min = find_min(root.right)
        root.val = right_min.val
        root.right = delete(root.right, root.val) # 注意，更新的这一点，要考虑各种情况，而不能只是将它变为nil
    return root

find_min(root):
    while root != nil and root.left != nil
        root = root.left
    return root

CPP实现，LeetCode 450. Delete Node in a BST

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    TreeNode* findMin(TreeNode* root) {
        while (root != NULL && root->left != NULL)
            root = root->left;
        return root;
    }
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == NULL)
            return root;
        if (key < root->val)
            root->left = deleteNode(root->left, key);
        else if (key > root->val)
            root->right = deleteNode(root->right, key);
        else {
            if (root->left == NULL)
                return root->right;
            if (root->right == NULL)
                return root->left;
            TreeNode* rightMin = findMin(root->right);
            root->val = rightMin->val;
            root->right = deleteNode(root->right, root->val);
        }
        
        return root;
    }
};

关于迭代的方式去实现删除的话，可能要比递归考虑更多的东西，但是想法的话还是很直观的，遍历查找要删除的节点时，始终记得记录其父节点。具体的删除过程与上述的大同小异，可能会有好多边界需要考虑。

建立

从数组

给定结构

确定一个二叉树，有两个要素，一个是二叉树的结构，另一个是各个节点的值，给定的数组确定了BST的值，但结构是未定的，根据给定的结构，可以构建一个确定的BST。

PAT 1099. Build A Binary Search Tree

根据二叉树的性质：中序遍历的输出顺序为升序。
先建立了二叉树结构之后，再进行中序遍历填入值就可以了。

以下为自己的代码，但是部分正确，有段错误！！！自己还没有找到错误所在。

#include <iostream>
#include <stack>
#include <algorithm>
#include <queue>
#include <vector>

using namespace std;

struct Node {
    int val;
    Node *left;
    Node *right;

    Node() : val(0), left(NULL), right(NULL) {}

    explicit Node(int val) : val(val), left(NULL), right(NULL) {}
};

void printTree(Node *root, int level) {
    if (root != NULL) {
        cout << root->val << endl;
        if (!(root->left == NULL && root->right == NULL)) {
            for (int i = 0; i < level + 1; ++i) {
                cout << "   ";
            }
            cout << "L->";
            printTree(root->left, level + 1);
            for (int i = 0; i < level + 1; ++i) {
                cout << "   ";
            }
            cout << "R->";
            printTree(root->right, level + 1);
        }
    } else {
        cout << "NULL" << endl;
    }
}

void levelOrderTravel(Node *root) {
    if (!root)
        return;
    cout << root->val;
    queue<Node *> q;
    if (root->left)
        q.push(root->left);
    if (root->right)
        q.push(root->right);
    while (!q.empty()) {
        Node *node = q.front();
        q.pop();
        cout << " " << node->val;
        if (node->left)
            q.push(node->left);
        if (node->right)
            q.push(node->right);
    }
}

int main() {
    Node *root = new Node(0);
    int nodeNum;
    cin >> nodeNum;
    if (nodeNum == 0)
        return 0;
    stack<Node *> s;
    s.push(root);
    for (int i = 0; i < nodeNum; ++i) {
        int l, r;
        cin >> l >> r;
        Node *node = s.top();
        s.pop();
        if (r != -1) {
            node->right = new Node(r);
            s.push(node->right);
        }
        if (l != -1) {
            node->left = new Node(l);
            s.push(node->left);
        }
    }

    vector<int> vals;
    for (int i = 0; i < nodeNum; ++i) {
        int v;
        cin >> v;
        vals.push_back(v);
    }

    sort(vals.begin(), vals.end());

//    printTree(root, 0);

    vector<Node *> nodes;
    stack<Node *> s1;

    Node *curr = root;

    while (!s1.empty() || curr != NULL) {
        while (curr != NULL) {
            s1.push(curr);
            curr = curr->left;
        }

        curr = s1.top();
        s1.pop();
        nodes.push_back(curr);
        curr = curr->right;
    }

    for (int i = 0; i < nodes.size(); ++i) {
        nodes[i]->val = vals[i];
    }

    levelOrderTravel(root);

    return 0;
}

平衡二叉树

如果限定是生成一个平衡二叉树的话，需要保证两边的相对均衡，将数组排序之后，每次取中点就可以做到：

LeetCode 108. Convert Sorted Array to Binary Search Tree

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if (nums.empty())
            return NULL;
        int midIdx = nums.size() / 2;
        TreeNode *node = new TreeNode(nums[midIdx]);
        if (midIdx == 0) {
            node->left = NULL;
        } else {
            vector<int> left(nums.begin(), nums.begin() + midIdx);
            node->left = sortedArrayToBST(left);
        }
        
        if (midIdx == nums.size() - 1) {
            node->right = NULL;
        } else {
            vector<int> right(nums.begin() + midIdx + 1, nums.end());
            node->right = sortedArrayToBST(right);            
        }
        return node;
    }
};

完全二叉树

完全二叉树的结构是确定的，所以仍然可以采用从给定结构构建二叉树的方法：

PAT 1064. Complete Binary Search Tree

我在PAT上的解答，部分正确！！有内存超限的错误！！！唔，怎么在PAT上做的这两道题，都有各种各样奇怪的错误，唉，有时间再看吧。

//
// Created by Zhao Xiaodong on 2018/2/1.
//

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <stack>

using namespace std;

struct Node {
    int val;
    Node *left;
    Node *right;

    Node() : val(0), left(NULL), right(NULL) {}
};

void levelOrderTravel(Node *root) {
    if (!root)
        return;
    cout << root->val;
    queue<Node *> q;
    if (root->left)
        q.push(root->left);
    if (root->right)
        q.push(root->right);
    while (!q.empty()) {
        Node *node = q.front();
        q.pop();
        cout << " " << node->val;
        if (node->left)
            q.push(node->left);
        if (node->right)
            q.push(node->right);
    }
}

int main() {
    int size;
    cin >> size;
    if (size == 0)
        return 0;
    vector<int> vals;
    for (int i = 0; i < size; ++i) {
        int v;
        cin >> v;
        vals.push_back(v);
    }

    sort(vals.begin(), vals.end());

    Node *root = new Node();

    queue<Node *> q;
    q.push(root);

    int nodeNum = 1;
    while (true) {
        Node *node = q.front();
        q.pop();
        node->left = new Node();
        nodeNum++;
        if (nodeNum == size)
            break;
        node->right = new Node();
        nodeNum++;
        if (nodeNum == size)
            break;
        q.push(node->left);
        q.push(node->right);
    }

    vector<Node *> nodes;
    stack<Node *> s1;

    Node *curr = root;

    while (!s1.empty() || curr != NULL) {
        while (curr != NULL) {
            s1.push(curr);
            curr = curr->left;
        }

        curr = s1.top();
        s1.pop();
        nodes.push_back(curr);
        curr = curr->right;
    }

    for (int i = 0; i < nodes.size(); ++i) {
        nodes[i]->val = vals[i];
    }

    levelOrderTravel(root);

    return 0;
}

参考了网上某篇博文的这道题的答案，发现自己这样写有点傻，利用性质完全二叉树的相关性质，可以更加简便和巧妙的完成这道题。

因为最后要求层级遍历，而完全二叉树的层级遍历有个性质可以利用：
按层遍历的输出顺序，就是用表示完全二叉树的数组中的顺序

这看起来并没有什么，但和我们知道的一个完全二叉树非常熟悉的性质：
leftIndex = 2 x rootIndex, rightIndex = 2 x rootIndex + 1

这样一来，便可以用下表来定位某个元素，而用数组的数据结构存储二叉树，其实遍历的行为更加简单，比如本题中用到的中序遍历：

void inorderTravel(int root) {
    if (root > size)
        return;
    inorderTravel(root * 2);
    inorderNodes.push_back(root);
    inorderTravel(root * 2 + 1);
}

完整解答：

//
// Created by Zhao Xiaodong on 2018/2/2.
//

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;

const int MAX = 1000;

int size;
vector<int> inorderNodes;

void inorderTravel(int root) {
    if (root > size)
        return;
    inorderTravel(root * 2);
    inorderNodes.push_back(root);
    inorderTravel(root * 2 + 1);
}

int main() {
    cin >> size;
    vector<int> vals;
    for (int i = 0; i < size; ++i) {
        int v;
        cin >> v;
        vals.push_back(v);
    }
    sort(vals.begin(), vals.end());

    inorderTravel(1);

    vector<int> tree(MAX + 1);

    for (int i = 0; i < size; ++i) {
        tree[inorderNodes[i]] = vals[i];
    }

    for (int i = 1; i < size; ++i) {
        cout << tree[i] << " ";
    }
    cout << tree[size];

    return 0;
}

从序列

从前序中序构建

前序中找到第一个节点，即为根节点，在中序中找到，中序的左侧就是左子树，右侧为右子树；得到左右子树的节点数量之后，可以将前序数组剩下的元素分成左右子树，进而递归的做下去。

LeetCode 105. Construct Binary Tree from Preorder and Inorder Traversal

（发现自己之前CPP和Python都AC过，python似乎看起来更简洁，要不以后做OJ都用PY？）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        if not inorder:
            return
        root_val = preorder.pop(0)
        root_idx = inorder.index(root_val)
        root = TreeNode(root_val)
        root.left = self.buildTree(preorder, inorder[0:root_idx])
        root.right = self.buildTree(preorder, inorder[root_idx + 1:])
        return root

从后序中序构建

与从前中构建很类似，做一个镜像即可：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, inorder, postorder):
        """
        :type inorder: List[int]
        :type postorder: List[int]
        :rtype: TreeNode
        """
        if not inorder:
            return
        val = postorder.pop()
        idx = inorder.index(val)
        root = TreeNode(val)
        root.right = self.buildTree(inorder[idx + 1:], postorder)
        root.left = self.buildTree(inorder[:idx], postorder)
        return root

前中转后与后中转前

有的时候，只要求通过前中序列写出后序，或者后中序列，写出前序，而不要求构建BST，这个时候可以更简便的完成而不用做多余的工作：

def pre_in_to_post(preorder, inorder):
    postorder = []
    if not preorder or not inorder:
        return postorder
    val = preorder[0]
    idx = inorder.index(val)
    postorder += pre_in_to_post(preorder[1:1 + idx], inorder[:idx])
    postorder += pre_in_to_post(preorder[1 + idx:], inorder[idx + 1:])
    postorder += [val]
    return postorder


def post_in_to_pre(postorder, inorder):
    preorder = []
    if not postorder or not inorder:
        return preorder
    val = postorder[-1]
    idx = inorder.index(val)
    preorder += [val]
    preorder += post_in_to_pre(postorder[:idx], inorder[:idx])
    preorder += post_in_to_pre(postorder[idx:-1], inorder[idx + 1:])
    return preorder


preorder = [3, 9, 20, 15, 7]
inorder = [9, 3, 15, 20, 7]
postorder = [9, 15, 7, 20, 3]

print(pre_in_to_post(preorder, inorder))
print(post_in_to_pre(postorder, inorder))

output:

[9, 15, 7, 20, 3]
[3, 9, 20, 15, 7]

---

参考：

http://blog.csdn.net/simple_the_best/article/details/52713491
http://www.cnblogs.com/jackwang822/p/4749965.html