平衡二叉树之AVL tree

Posted on | Edited on | In |

定义

AVL tree是一个BST对于每一个节点，左子树和右子树的高度差不超过1（空树高度为-1）

这里需要明确，高度的定义：

维基百科：
Height of node
The height of a node is the number of edges on the longest path between that node and a leaf.
Height of tree
The height of a tree is the height of its root node.

树的平衡维护

对一棵平衡的树，进行插入或删除可能改变树的平衡性，这里只考虑插入，删除类似（虽然稍微麻烦一点）。

对于节点X，插入一个节点导致其不平衡，会有四种情况：

  • 新增加的节点是其左结点的左子树
  • 新增加的节点是其左结点的右子树
  • 新增加的节点是其右结点的右子树
  • 新增加的节点是其右结点的左子树

后两种情况与前两种镜像，不作考虑，所以是由两种情况，称之为LL(Left-Left)问题和LR(Left-Right)问题

LL

-w635

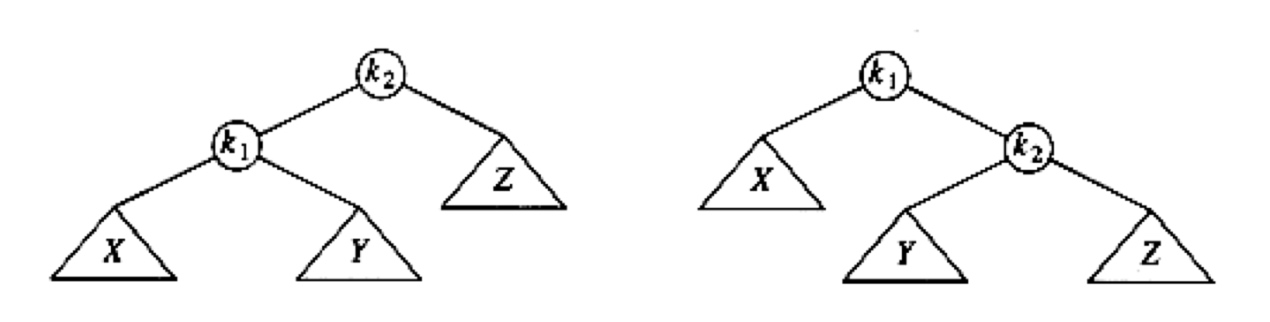
当插入到X，导致$k_1$的的高度 > Z的高度+2的时候，树不平衡！

这时候要做的是想办法，把X提上去，把Z压下来，这里需要做的是从左图到右图的变形，这样的形变也叫做一次旋转。

这里有一个动态演示的网站：https://www.cs.usfca.edu/~galles/visualization/AVLtree.html 显示了旋转的动画效果，非常直观

初始：

-w599

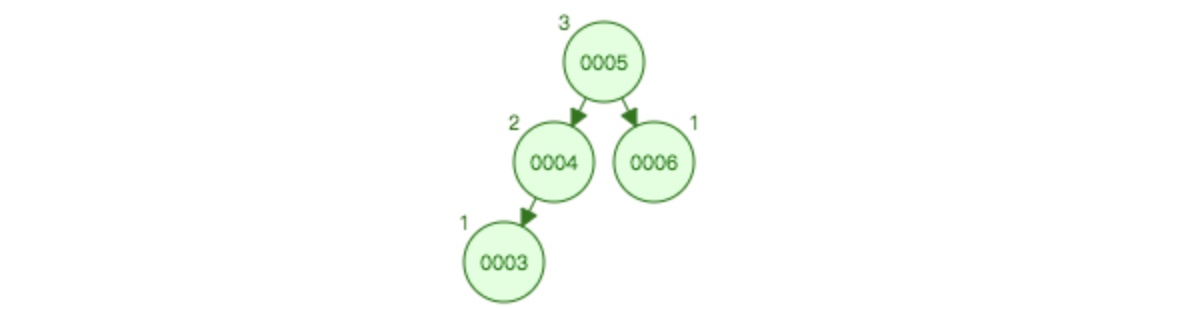
插入2之后：

-w599

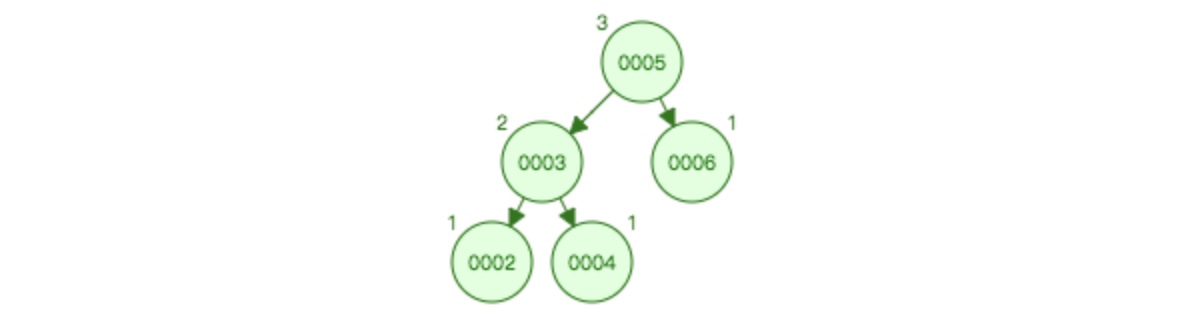
再次插入1之后：

-w602

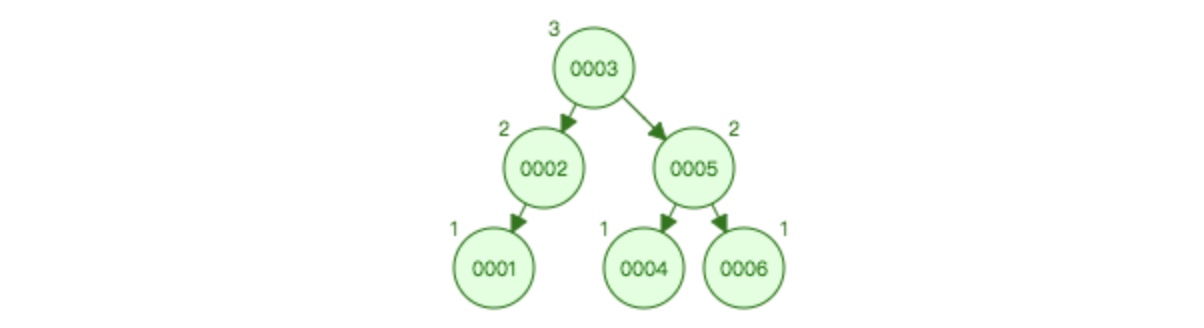
这里树的结构变动比较大，因为不是3结点不平衡，而是根节点5不平衡，所以是5和3旋转，根节点发生改变。

LR

-w656

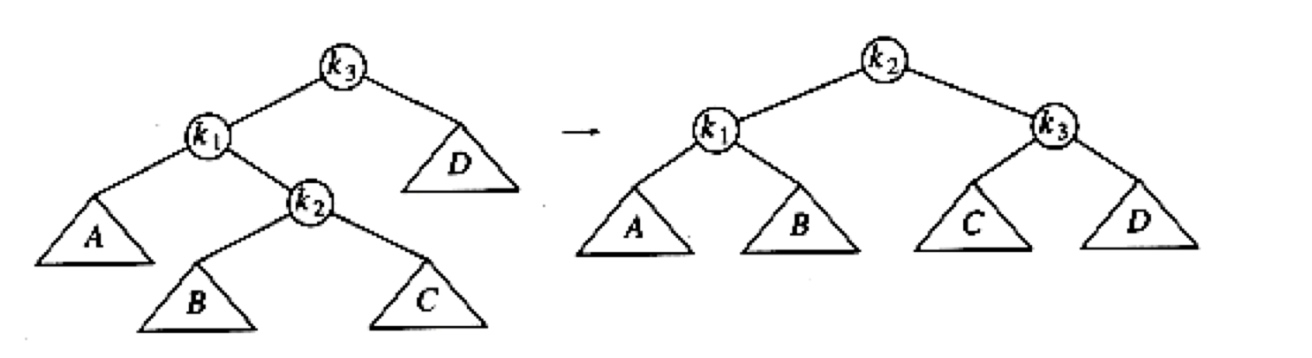
很巧妙的一个变形！

在$k_1$的右子树中插入了东西，导致$k_3$不平衡，现在是要把$k_1$的右子树也就是$k_2$提上去，把D压下去，需要通过两次旋转，就是先$k_1$-$k_2$的一次RR旋转，再$k_2$-$k_3$的一次LL旋转，但是我通常都不想这样记，直接记住这个形式，下边那个从中间“穿过去”，然后原来的左右子树变为新的子树的右左子树。

例子就不举了。

树的平衡化

上述的两个旋转，是平衡化的两个基本操作，平衡化的变形肯定属于这两者。

如果是新的节点插入一棵已经平衡的树的话，用递归的方式非常直观，大概：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def insert(X, T):
    if T == null:
        place here
    else:
        if X < T.val:
            insert(X, T.left)
            if not balence:
                if is LL:
                    LLrotate
                else:
                    LRrotate
        else:
            insert(X, T.right)
            if not balence:
                if is RR:
                    RRrotate
                else:
                    RLrotate
    update height # don't forget, we use height to check balence

插入操作的实现

PAT-A 1066 Root of AVL Tree

https://pintia.cn/problem-sets/994805342720868352/problems/994805404939173888

-w975

-w990

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
//
// Created by Zhao Xiaodong on 2018/8/22.
//
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
struct Node {
    int val;
    Node *left;
    Node *right;
    int height;
    Node(int val) : val(val), left(nullptr), right(nullptr) {}
};
int getHeight(Node *root) {
    if (!root)
        return -1;
    return root->height;
}
Node *llRotate(Node *root) {
    Node *newRoot = root->left;
    root->left = newRoot->right;
    newRoot->right = root;
    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;
    return newRoot;
}
Node *rrRotate(Node *root) {
    Node *newRoot = root->right;
    root->right = newRoot->left;
    newRoot->left = root;
    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;
    return newRoot;
}
Node *lrRotate(Node *root) {
    Node *newRoot = root->left->right;
    root->left->right = newRoot->left;
    newRoot->left = root->left;
    root->left = newRoot->right;
    newRoot->right = root;
    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    newRoot->left->height = max(getHeight(newRoot->left->left), getHeight(newRoot->left->right)) + 1;
    newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;
    return newRoot;
}
Node *rlRotate(Node *root) {
    Node *newRoot = root->right->left;
    root->right->left = newRoot->right;
    newRoot->right = root->right;
    root->right = newRoot->left;
    newRoot->left = root;
    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    newRoot->right->height = max(getHeight(newRoot->right->left), getHeight(newRoot->right->right)) + 1;
    newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;
    return newRoot;
}
Node *insert(Node *root, int k) {
    if (!root) {
        Node *node = new Node(k);
        node->height = 0;
        return node;
    }
    if (k < root->val) {
        root->left = insert(root->left, k);
        if (getHeight(root->left) - getHeight(root->right) == 2) {
            if (k < root->left->val)
                root = llRotate(root);
            else
                root = lrRotate(root);
        }
    } else {
        root->right = insert(root->right, k);
        if (getHeight(root->right) - getHeight(root->left) == 2) {
            if (k < root->right->val)
                root = rlRotate(root);
            else
                root = rrRotate(root);
        }
    }
    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    return root;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int N;
    cin >> N;
    Node *root = nullptr;
    for (int i = 0; i < N; i++) {
        int k;
        cin >> k;
        root = insert(root, k);
    }
    cout << root->val;
    return 0;
}

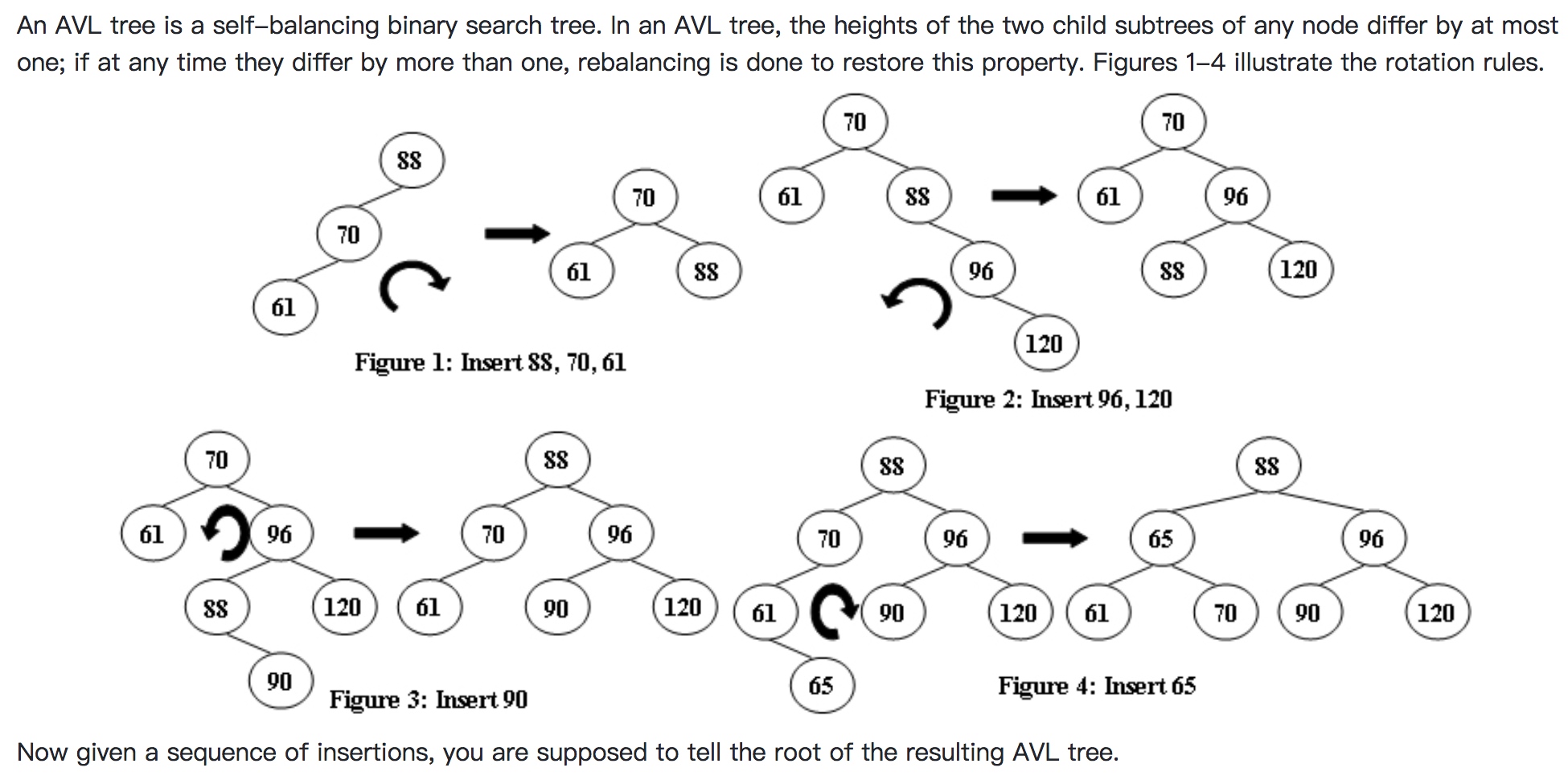
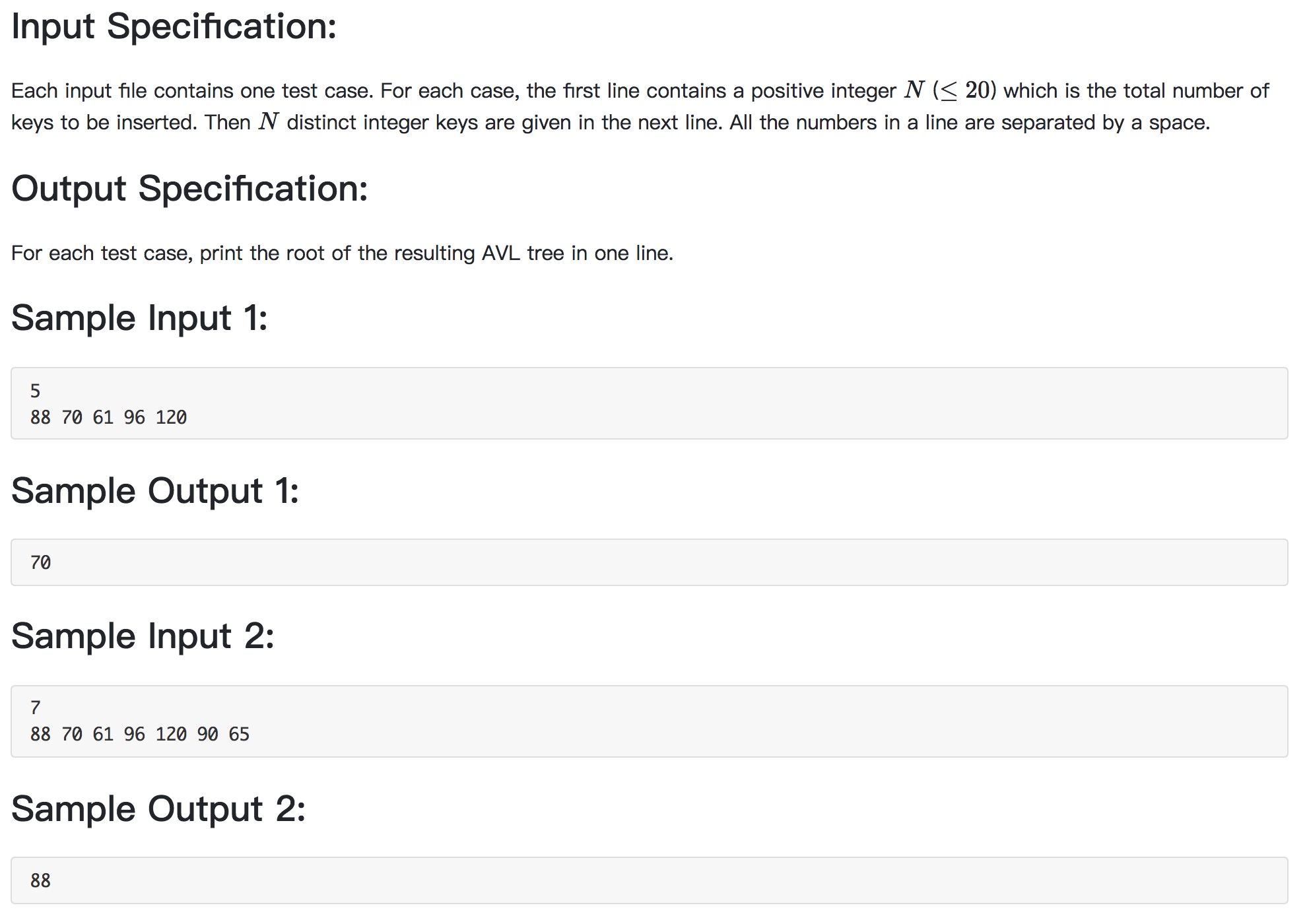
不要眼高手低啊！！！算法思想，和实现出来，中间的差距，就是你想要提高的所谓的编程能力，或者码力！如果眼高手低，总觉得自己肯定能实现出来，一定会吃亏的！！！