287. Find the Duplicate Number

Posted on | In , |

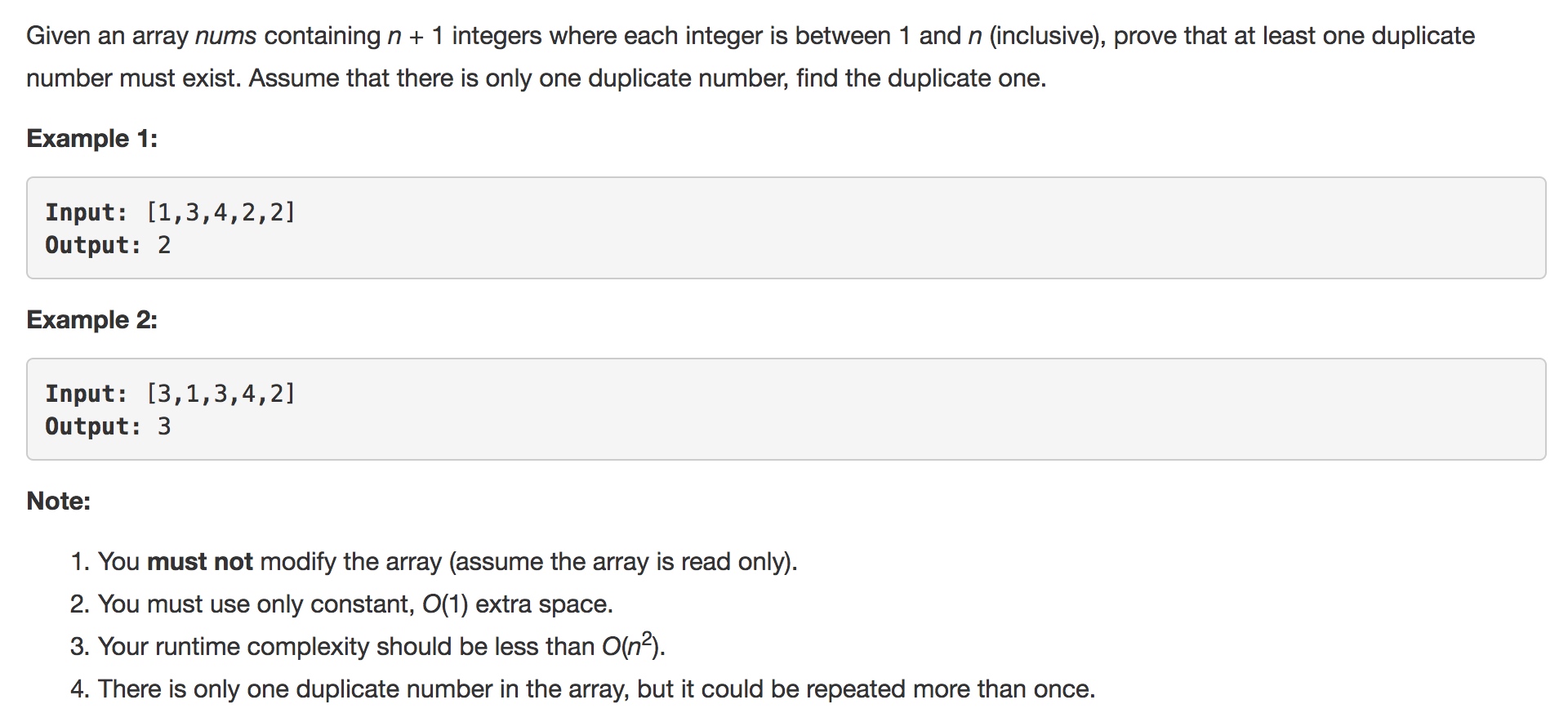
题目

https://leetcode.com/problems/find-the-duplicate-number/description/

-w960

想法

一时没有想出解决办法..

遍历然后二分查找嘛？不可行啊，乱序的

好像xor有用，相同的数xor之后是0，重复次数不定，好像也不好用

题目中强调了1-n，n+1个数，是不是可以利用？

如果分治的话，一侧相同的，左右存在相同的，关键是怎么判断啊

不成，sort，nlogn，然后遍历？好傻，题目规定不能动数组

Cycle detection

可以把问题归约到检测环的问题上！

题目中强调了1 - n, n + 1个数，意思是数在数组的下标范围内。按照下标进行搜寻，如果有重复的值，便会出现环。

检测环的方法，有多种，参见：https://en.wikipedia.org/wiki/Cycle_detection

Floyd’s Tortoise and Hare

思想大致是这样的：让龟兔从同一起点出发，但以不同的速度前进，如果路径没有环的话，那么当兔子走到尽头，龟兔是不会相遇的，如果相遇了，说明成环。

所以这道题，用这样的方式就可以了~

不过，判断除了相交的位置，并不能知道重复的在哪里。

不过，这里不作过多的讨论，有另外的典型题目来讨论这个问题：https://leetcode.com/problems/linked-list-cycle-ii/discuss/44781/Concise-O(n)-solution-by-using-C++-with-Detailed-Alogrithm-Description

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int tortoise = 0, hare = 0;
        do {
            tortoise = nums[tortoise];
            hare = nums[nums[hare]];
        } while(nums[tortoise] != nums[hare]);
        
        int p1 = 0, p2 = tortoise;
        while (nums[p1] != nums[p2]) {
            p1 = nums[p1];
            p2 = nums[p2];
        }
        return nums[p1];
    }
};

第一个循环，找到了相遇的点，第二个循环利用了起点走到环起点=相遇点走到环起点这一特性：

It can be concluded that the distance between the head location and entry location is equal to the distance between the meeting location and the entry location along the direction of forward movement.