Median of Two Sorted Arrays

题目

https://leetcode.com/problems/median-of-two-sorted-arrays/description/

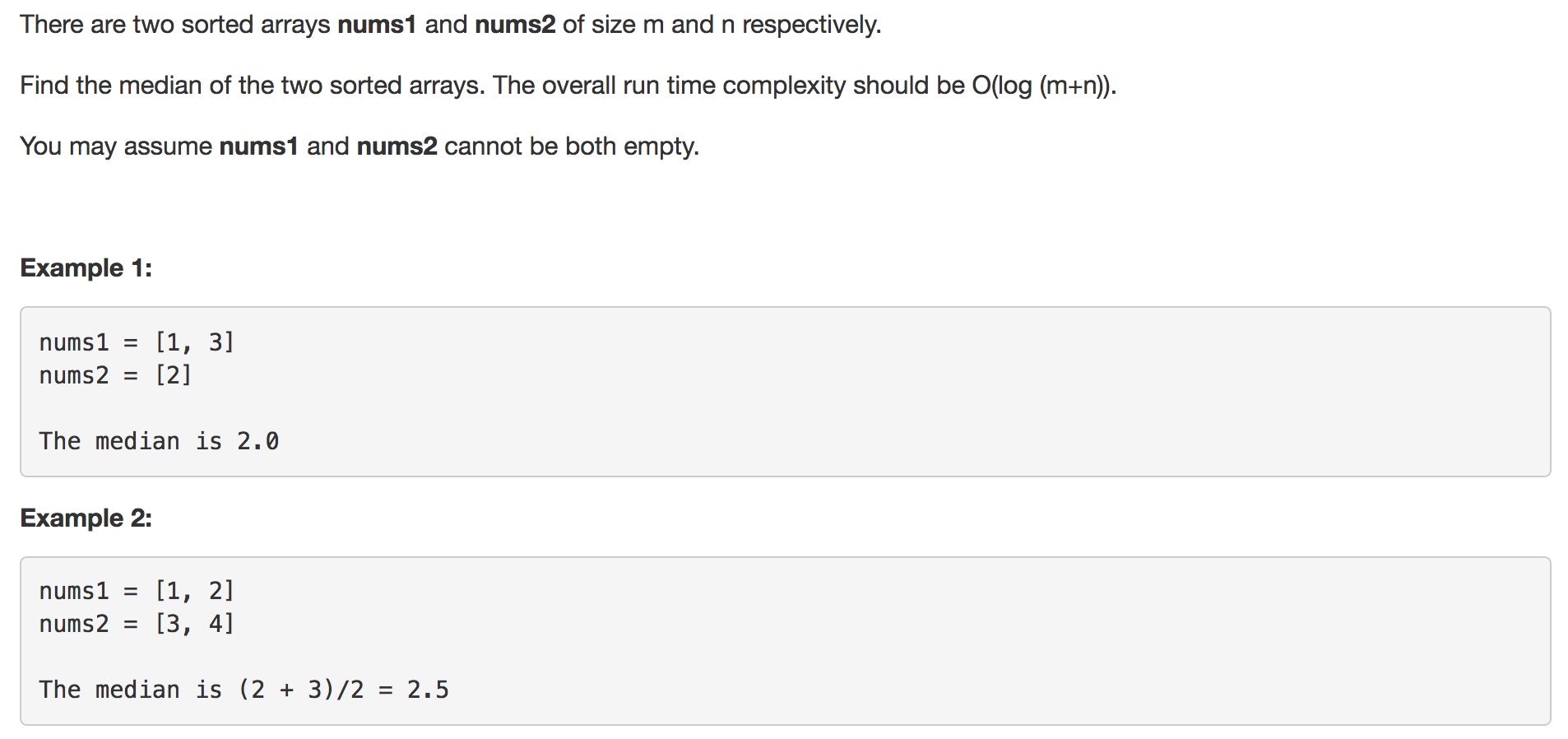
想法

时间复杂度，要求很高

其实这道题，空间复杂度，也可以要求很高，PAT有一道类似的题：

https://pintia.cn/problem-sets/994805342720868352/problems/994805466364755968

---

leetCode上的solution:
https://leetcode.com/problems/median-of-two-sorted-arrays/solution/

总结下来，思想就是，根据中位数的定义，把两个数组各自分成两个部分，两个左侧部分是合并后的左侧，右侧部分是合并后的右侧。然后，根据两遍相等的关系，找到两者下标的关系，然后将两个变量化为一个变量，这样一来，二分就好了。

具体来看：

n1.size: M
n2.size: N

要找到i, j，满足：

分成两个部分：

n1[0] ~ n1[i - 1]; n1[i] ~ n1[M - 1]
n2[0] ~ n2[j - 1]; n2[j] ~ n2[N - 1]

1. i + j == M-i + N-j || i + j == M-i + N-j + 1
2. n1[i - 1] <= n2[j] && n2[j - 1] <= n1[i]

这样一来，也就是说: j = (M + N - 2 * i + 1) / 2

(这里默认N>=M，这样可以保证 j >= 0)

然后，找i即可
用二分查找的方式，验证是否满足条件2，找到最后的i

这样一来，没有占用额外的空间，O(1)复杂度
时间复杂度，二分查找，较小的那个数组，应该是O(log(min(m, n)))

答案

自己写的一个答案，边界情况考虑的很不优雅，最后是对着LeetCode的测试点一个一个改才AC了hhh

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        vector<int>& n1 = nums1.size() > nums2.size() ? nums2 : nums1;
        vector<int>& n2 = nums1.size() > nums2.size() ? nums1 : nums2;
        int M = n1.size(), N = n2.size();
        int l = 0, r = n1.size();
        // cout << l << " " << r;
        int i = 0, j = (M + N + 1) / 2;
        while (l <= r) {
            i = (l + r) / 2;
            j = (M + N - 2 * i + 1) / 2;
            // cout << i << " " << j << endl;
            if ((i <= 0 || j >= N || n1[i - 1] <= n2[j]) && (j <= 0 || i >= M || n2[j - 1] <= n1[i])) {
                break;
            } else if ((i > 0 && j >= N) || n1[i - 1] > n2[j]) {
                r = i - 1;
            } else {
                l = i + 1;
            }
            // cout << l << " " << r << endl;
        }
        cout << endl << i << " " << j;
        if ((M + N) % 2 == 1) {
            if (i == 0)
                return n2[j - 1];
            if (j == 0)
                return n1[i - 1];
            return (double)max(n1[i - 1], n2[j - 1]);
        } else {
            if (n1.empty()) {
                return (double)(n2[j - 1] + n2[j]) / 2;
            }
            return (double)(max(i > 0 ? n1[i - 1] : INT_MIN, j > 0 ? n2[j - 1] : INT_MIN) + min(i < M ? n1[i] : INT_MAX, j < N ? n2[j] : INT_MAX)) / 2;
        }
    }
};