Posted on | Edited on | In , |

题目

https://leetcode.com/problems/predict-the-winner/description/

想法

DP 算出num[x][y]

1
2
3
4
num[0][0] = n[0]
num[0][1] = max(n[0][0], n[1][1])
...
num[x][y] = max(n[x] + sum[x+1][y] - num[x+1][y], n[y] + sum[x][y-1] - num[x][y-1])

先算 num[i][i]
再算 num[i-1][i]
最后 num[0][N]

答案

虽然想的过程有些不顺利，但是一遍AC了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    bool PredictTheWinner(vector<int>& nums) {
        int m[20][20] = {0};
        int sum[20][20] = {0};
        for (int i = 0; i < nums.size(); i++) {
            for (int j = 0, k = i; k < nums.size(); j++, k++) {
                if (j == k) {
                    m[j][k] = sum[j][k] = nums[j];
                } else {
                    sum[j][k] = sum[j][k - 1] + nums[k];
                    m[j][k] = max(nums[j] + sum[j+1][k] - m[j + 1][k], nums[k] + sum[j][k - 1] - m[j][k - 1]);
                }
            }
        }
        
        return m[0][nums.size() - 1] >= sum[0][nums.size() - 1] - m[0][nums.size() - 1];
    }
};

回顾

DP的题目，一般是想出来基本就比较容易了

这个题目的DP不是从最小到最大，也不是从最大到最小（不是一行一行的推进或者一列一列的推进），而是从对角线开始，向上推进的，也算是一种比较新的思路吧

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/remove-element/description/

想法

没有什么想法，用了erase函数
应该有更好的想法的

答案

我的

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
		for (int i = 0; i < nums.size(); i++) {
            if (nums[i] == val) {
                nums.erase(nums.begin() + i);
                i--;
            }
        }
        return nums.size();
    }
};

一个他人的答案，值得参考：

1
2
3
4
5
6
7
8
9
10
int removeElement(vector<int>& nums, int val) {
    int cnt = 0;
    for(int i = 0 ; i < nums.size() ; ++i) {
        if(nums[i] == val)
            cnt++;
        else
            nums[i-cnt] = nums[i];
    }
    return nums.size()-cnt;
}

回顾

都是奇技淫巧，不考算法，全都是奇技淫巧！

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/longest-palindrome/description/

想法

easy级的题目，统计奇偶就可以了

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int longestPalindrome(string s) {
        vector<int> num(52);
        for (char c : s) {
            int i = c >= 'a' ? c - 'a' + 26 : c - 'A';
            num[i]++;
        }
        int len = 0;
        bool oddFlag = false;
        for (int i = 0; i < num.size(); i++) {
            if (num[i] % 2 == 0)
                len += num[i];
            else
                if (oddFlag == false) {
                    len += num[i];
                    oddFlag = true;
                } else {
                    len += num[i] - 1;
                }
        }
        return len;
    }
};

回顾

可以尝试用其它语言，如JS，Python，Swift等语言来解决问题来锻炼语言掌握的熟练度

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/remove-nth-node-from-end-of-list/description/

想法

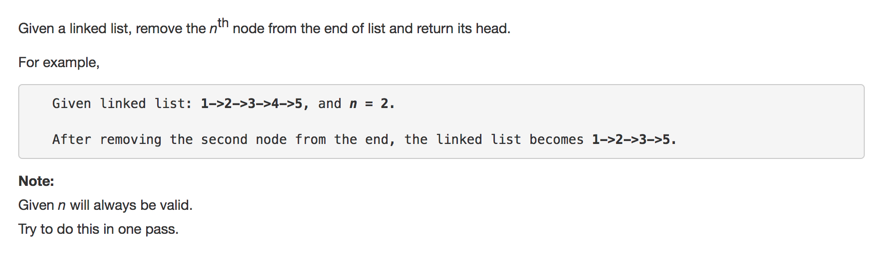
比较简单，就是记录着扫着的ptr之前n位的地址就可以了。

答案

一次AC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* target = head;
        ListNode* ptr = head;
        for (int i = 0; i < n; i++) {
            ptr = ptr->next;
        }
        if (ptr == NULL) {
            ListNode* tmp = head;
            head = head->next;
            free(tmp);
            return head;
        }
        while(ptr->next != NULL) {
            ptr = ptr->next;
            target = target->next;
        }
        ListNode* tmp = target->next;
        target->next = tmp->next;
        free(tmp);
        return head;
    }
};

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/sum-of-two-integers/description/

想法

最初想的是用CLA的方式，但是发现用位运算并不好算p_i，遂放弃，后选择用密码学课上学到的提取单个位的方法进行处理，做位的加法

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int getSum(int a, int b) {
        int helper = 1;
        int result = 0;
        int c = 0;
        for (int i = 0; i < sizeof(int) * 8; i++) {
            int aBit = a & helper, bBit = b & helper, cBit = c & helper;
            result |= (aBit ^ bBit ^ cBit);
            if (!!(aBit & bBit | aBit & cBit | bBit & cBit))
                c = (helper << 1);
            else
                c = 0;
            helper <<= 1;
        }
        if (!!c)
            result |= c;
        return result;
    }
};

感想

虽然是一道Easy级的题目，但是自己也是花费了不小的功夫。
主要是调bug上，考虑不周，在进位的处理上有些考虑不全，WA了好几次。

位操作还是值得学习一下的。

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/largest-divisible-subset/description/

想法

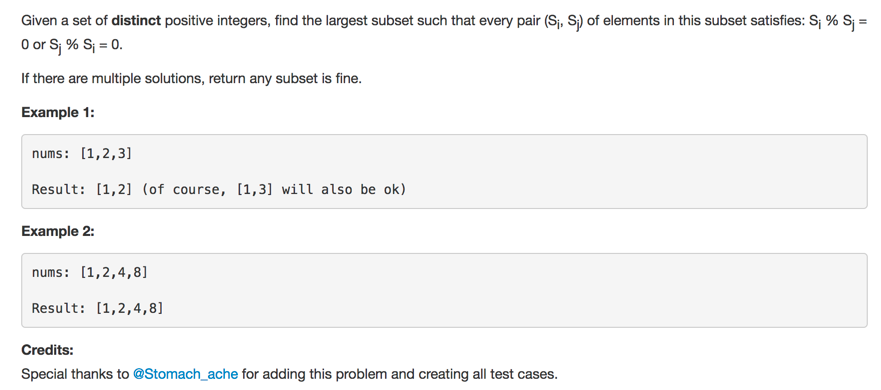
没有什么思路…或许贪心？

不，应该可以从数学的角度上解决的。
如果能任意地被整除，需要满足什么条件呢？
每添加进一个，都可以被这个set中的每一个整除
这样一来，是个O(n^2 )的复杂度，可以吗？
先试试吧
不对，不是O(n^2 )，排序需要nlog n，因为已经序的了，应该只用O(n k)，k是set的数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<int> largestDivisibleSubset(vector<int>& nums) {
        if (nums.empty())
            return vector<int>();
        std::sort(nums.begin(), nums.end());
        vector<vector<int>> sets;
        bool inserted = false;
        int maxSize = 1;
        int maxSizeIdx = 0;
        for (int i = 0; i < nums.size(); ++i) {
            for (int j = 0; j < sets.size(); ++j) {
                if (nums[i] % sets[j][sets[j].size() - 1] == 0) {
                    sets[j].push_back(nums[i]);
                    if (maxSize < sets[j].size()) {
                        maxSize = sets[j].size();
                        maxSizeIdx = j;
                    }
                    inserted = true;
                    break;
                }
            }
            if (inserted == false) {
                vector<int> vec;
                sets.push_back(vec);
                sets[sets.size() - 1].push_back(nums[i]);
            } else {
                inserted = false;
            }
        }
        return sets[maxSizeIdx];
    }
};

嗯，看来自己本来有一些Naive了

没有考虑到这样的情况
那看来原来的想法是不行的
一个更明显的例子：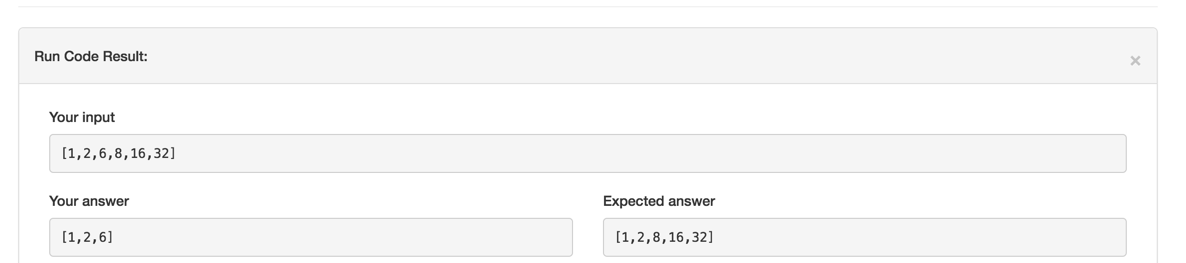

考虑用DP做
因为，大数可以表示成因式的和

看问题的样子，是很符合贪心的策略的，但是怎么用呢？
唔，有必要补一补基础知识了，唉，先看下答案吧，不想想了orz

尝试建一个多叉树
做完之后，调了好多bug，却发现也同样没有考虑到那个问题，唉，本质上和原来是一样的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//
// Created by Zhao Xiaodong on 2017/8/1.
//
#include <iostream>
#include <vector>
using namespace std;
class Solution {
    struct TreeNode {
        int val;
        vector<TreeNode*> children;
        TreeNode(int x) : val(x) {}
    };
    std::vector<int> result;
    std::vector<int> current;
    bool insert(TreeNode *tree, int num) {
        if (num % tree->val != 0)
            return false;
        bool inserted = false;
        current.push_back(tree->val);
        for (int i = 0; i < tree->children.size(); ++i) {
            if (insert((tree->children)[i], num)) {
                inserted = true;
            }
        }
        if (!inserted) {
            TreeNode *newNode = new TreeNode(num);
            (tree->children).push_back(newNode);
            current.push_back(num);
        }
        if (current.size() > result.size())
            result = current;
        current = vector<int>{};
        return true;
    }
public:
    vector<int> largestDivisibleSubset(vector<int>& nums) {
        if (nums.empty())
            return vector<int>();
        if (nums.size() == 1)
            return vector<int>{nums[0], };
        std::sort(nums.begin(), nums.end());
        TreeNode *tree = new TreeNode(1);
        for (int i = 0; i < nums.size(); ++i) {
            insert(tree, nums[i]);
        }
        result.erase(result.begin());
        return result;
    }
};

参考答案

哈？答案一票都是用DP的？？？

https://discuss.leetcode.com/topic/49456/c-solution-with-explanations

勉强看懂，看是不保证自己能写出来，这题就先放过吧，日后再做。

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/find-largest-value-in-each-tree-row/description/

想法

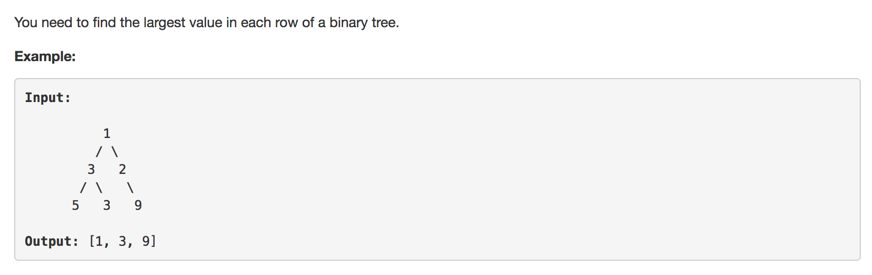
嗯，有一个vector来记录每一层的最大值，然后搜一遍树，更新最大值就可以了，应该就是这样

我的答案

一次AC了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> maxVal;
    vector<int> largestValues(TreeNode* root) {
        travel(root, 1);
        return maxVal;
    }
    void travel(TreeNode* node, int level) {
        if (node == NULL)
            return;
        if (maxVal.size() < level)
            maxVal.push_back(node->val);
        else if (node->val > maxVal[level - 1])
            maxVal[level - 1] = node->val;
        travel(node->left, level + 1);
        travel(node->right, level + 1);
    }
};

回顾

比较明确，比较简单吧。
不做多余的事，更新最大值就好了，难得有一题如此轻松地AC哈哈。

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/task-scheduler/description/

想法

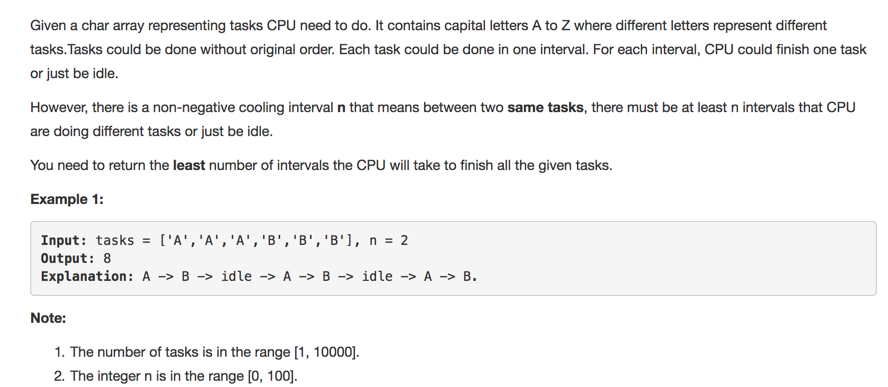
第一眼，感觉是Greedy

算了，想了半天，还是没有什么头绪
看答案吧

（LeetCode有答案好，也不好orz）

参考答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        std::unordered_map<char, int> map;
        int count = 0;
        for (auto t : tasks) {
            map[t]++;
            count = max(count, map[t]);
        }
        
        int num = (n + 1) * (count - 1);
        for (auto t : map) {
            if (t.second == count)
                num++;
        }
        
        return max((int)tasks.size(), num);
    }
};

回顾

自己本来的思路跟这个类似，就选择这个作为答案了
先找到最大的，然后拉一个框：(n+1)*(count-1),如果有超出的（最大的），刚+1
另外还要考虑task大，n小，框框放不下的情况，这样需要max(task.size(), num)

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/min-stack/description/

想法

比较简单，就用一个栈来记录原栈底到当前顶的最小值，每次push的时候决定是否放进栈里。

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class MinStack {
private:
    stack<int> minVal;
    stack<int> myStack;
public:
    /** initialize your data structure here. */
    MinStack() {
    }
    
    void push(int x) {
        if (minVal.empty() || x <= getMin())
            minVal.push(x);
        myStack.push(x);
    }
    
    void pop() {
        if (myStack.top() == minVal.top())
            minVal.pop();
        myStack.pop();
    }
    
    int top() {
        return myStack.top();
    }
    
    int getMin() {
        return minVal.top();
    }
};
/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

感想

自己想得有些多了。
其实本来只在push的时候判断下就可以了，因为如果没把第二小的push进去，第二小也会在最小之前pop，不会发生最小无法维护的情况。

Posted on | Edited on | In , |

题目

https://leetcode.com/problems/bulb-switcher/description/

想法

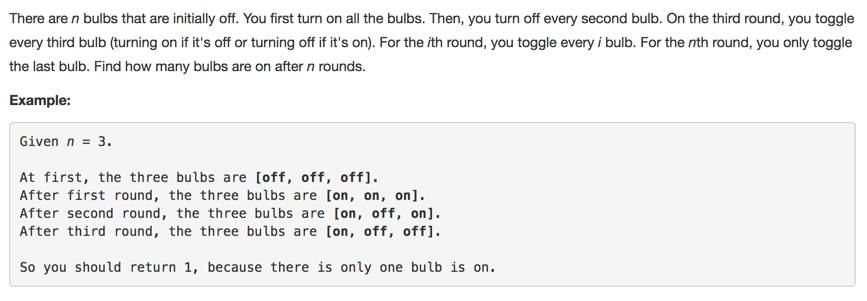
注意题意是toggle!

对一个数因式分解，如果不同的因式数量是奇数，则on；如果偶数，则off
1 : 1 on
2 : 1, 2 off
3 : 1, 3 off
4 : 1, 2, 4 on
…
8 : 1, 2, 4, 8 off
找到一个数的不同因数

Number of Factors of an Integer
http://www.cut-the-knot.org/blue/NumberOfFactors.shtml

$n = a^pb^q…c^r$
where a, b, c is prime

8: 2^3 3个+1个（1）
4: 2^2 2个+1
3: 3^1 1+1个
9: 1, 3, 9 — 3^2 2+1个
12: 1, 2, 3, 4, 6, 12 — 2^2 3^1 (2+1)(1+1)

所以最终得到：(p+1)(q+1)…(r+1)个，其中包括了其本身和1

转化为找到其素因数
先找出素数表，再除去就可以了

！！想错了，这只找出了最后一个灯的亮灭

看了高票的答案，自己想对了部分，但是关键的一点没有想到，就是只有完全平方数最后才会保持亮着！！！

一个答案

1
2
3
4
> int bulbSwitch(int n) {
>   return sqrt(n);
> }
>

A bulb ends up on iff it is switched an odd number of times.

Call them bulb 1 to bulb n. Bulb i is switched in round d if and only if d divides i. So bulb i ends up on if and only if it has an odd number of divisors.

Divisors come in pairs, like i=12 has divisors 1 and 12, 2 and 6, and 3 and 4. Except when i is a square, like 36 has divisors 1 and 36, 2 and 18, 3 and 12, 4 and 9, and double divisor 6. So bulb i ends up on if and only if i is a square.

So just count the square numbers.

Let R = int(sqrt(n)). That’s the root of the largest square in the range [1,n]. And 1 is the smallest root. So you have the roots from 1 to R, that’s R roots. Which correspond to the R squares. So int(sqrt(n)) is the answer. (C++ does the conversion to int automatically, because of the specified return type).

优秀！

回顾

这道题，自己最后还是没有想到，一道算是找规律的题吧，虽然自己发现了些道理，但是还是没有进一步的发现，加油吧！