题目
https://leetcode.com/problems/spiral-matrix-ii/description/

想法
其实就是考虑一些边界值,考虑的好,就写起来很简洁
还有四个方向的变化,怎么统一起来,一点小trick
答案
|
|
Coder love Design
https://leetcode.com/problems/spiral-matrix-ii/description/

其实就是考虑一些边界值,考虑的好,就写起来很简洁
还有四个方向的变化,怎么统一起来,一点小trick
|
|
https://leetcode.com/problems/sort-characters-by-frequency/description/


按照频率排序
如果用一个map来存放,sort一下就可以了
空间利用率有点高?
先写一个再说吧
|
|
虽然空间复杂度有点高,但是也AC了。
这里注意,自己本来想sort一个map,试了之后才知道cpp的map不能被sort,最便利的排序方式是转存到vector~
https://leetcode.com/problems/merge-intervals/description/

先排序,按照第一个数升序
挨个看是否可以合并
这样真的可以嘛,感觉好简单的样子,与赞数不符啊
咦,还真这样AC了,这水题,为什么900+的赞,不懂不懂
|
|
https://leetcode.com/problems/largest-divisible-subset/description/
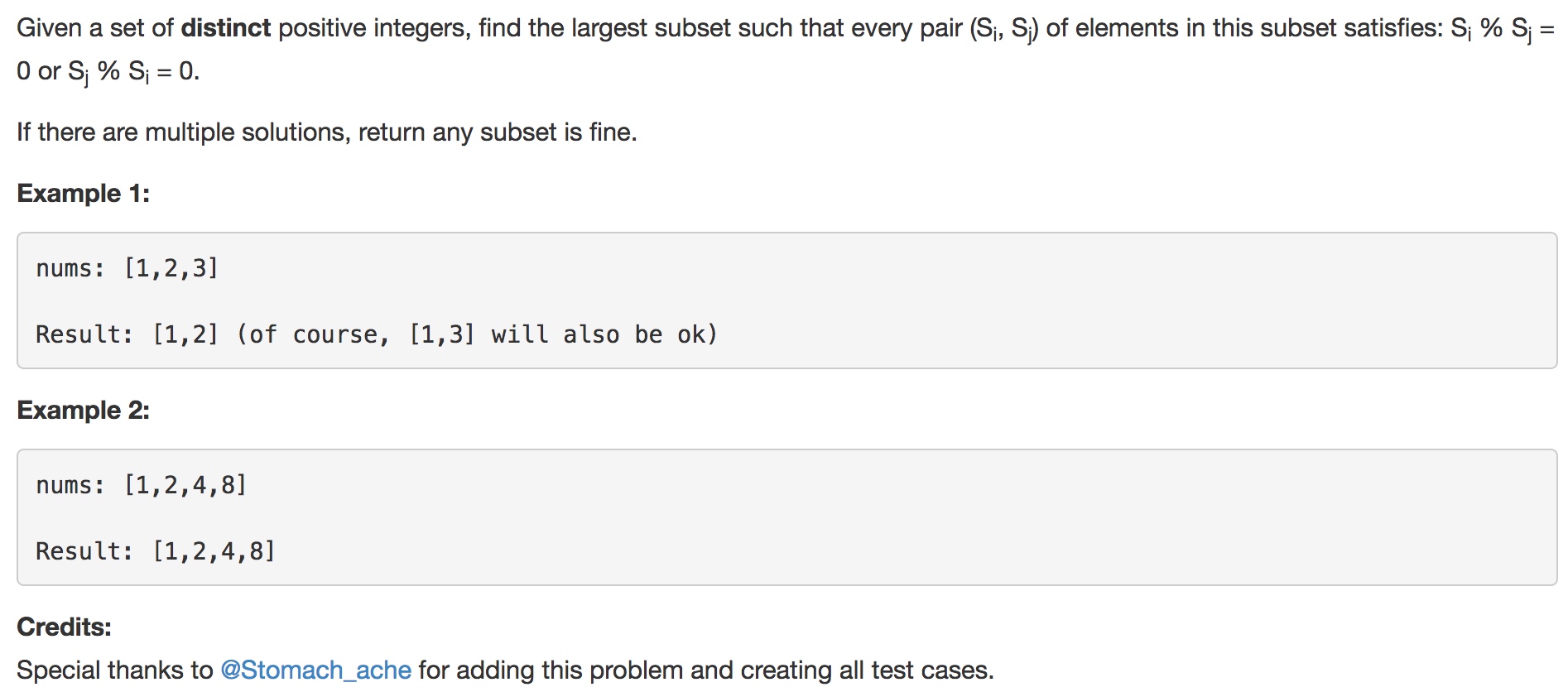
排序
能整除集合中的最大的数,那么也会属于这个集合
直觉DP..
遇到一个新数,从此数前一个开始判断,是否可以并入
维护更新max
好像需要回溯来做,需要记录序列
回溯写了个,TLE
|
|
感觉是剪枝做得不够充分..
1 2 4
1 2 之后,就不应该试1 4了,肯定比1 2..少
这个怎么剪呢?
将上述代码中#1部分改动:
|
|
AC,但是时间是1540ms,显然勉强AC
if (nums[i] % nums[j] == 0)
dp[i] = max(dp[j] + 1, dp[i])
最后运行16ms,还好
这里关键的一点是选取最后的结果上,注意筛选方式:
|
|
|
|
https://leetcode.com/problems/maximum-subarray/description/

很经典的一道题目,属于分治和DP的典型题目。
时间复杂度应该是O(nlogn),设计起来,如同题目中说的:subtle
TODO..
DP推导式:
dp[i] = max(dp[i - 1] + nums[i], nums[i])
|
|
简化之后,用O(1)的时间复杂度就可以:
|
|
https://pintia.cn/problem-sets/994805342720868352/problems/994805514284679168
1007 Maximum Subsequence Sum (25)(25 分)
Given a sequence of K integers { N~1~, N~2~, …, N~K~ }. A continuous subsequence is defined to be { N~i~, N~i+1~, …, N~j~ } where 1 <= i <= j <= K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.
Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.
Input Specification:
Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (<= 10000). The second line contains K numbers, separated by a space.
Output Specification:
For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.
Sample Input:
|
|
Sample Output:
|
|
记录左右下标,当更新max的同时更新下标
|
|
https://pintia.cn/problem-sets/994805342720868352/problems/994805523835109376
1003 Emergency (25)(25 分)
As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (<= 500) - the number of cities (and the cities are numbered from 0 to N-1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1, c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather.\ All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input
|
|
Sample Output
|
|
记下这道题,只是想熟悉一下,PAT中图的表示方式和处理。
这道题,还需要记录最短路径的数量,这一点需要注意!
|
|
https://leetcode.com/problems/longest-mountain-in-array/description/
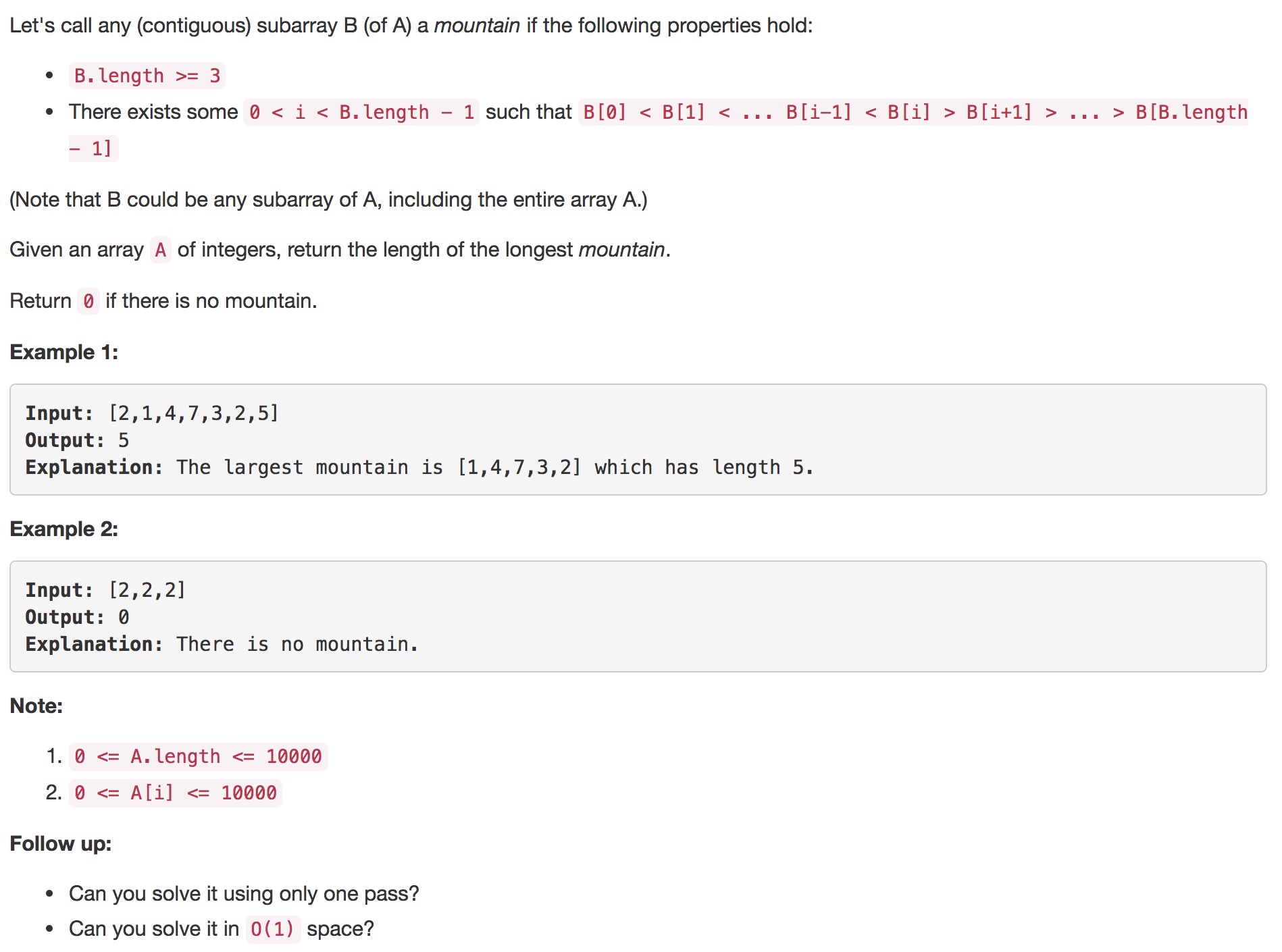
描述清楚不难,但是用一个巧妙简洁的方式叙述出来,可就没有那么容易了
蛮有趣的一个题目
|
|
https://leetcode.com/problems/merge-k-sorted-lists/description/
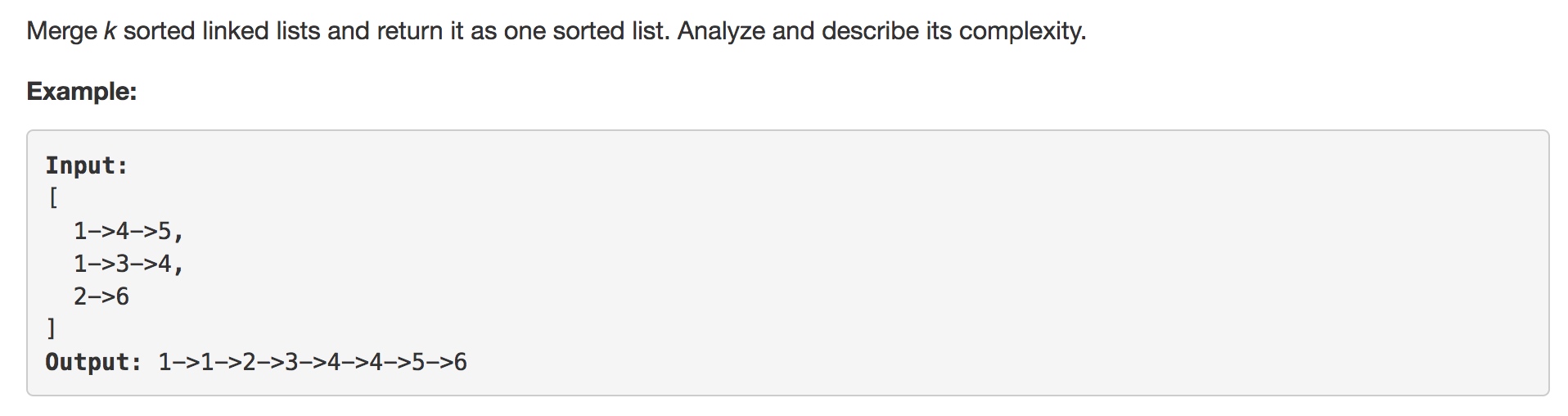
很经典的样子..
m个链表,每个链表长度为n数量级
循环找最小的,复杂度有O(m * n)
建堆可以做,但是怎么发挥排好序的是关键
两两合并也可以
TODO..
https://leetcode.com/problems/linked-list-cycle-ii/description/

由LeetCode287过来的
Concise O(n) solution by using C++ with Detailed Alogrithm Description
ngclAlogrithm Description:
Step 1: Determine whether there is a cycle
1.1) Using a slow pointer that move forward 1 step each time
1.2) Using a fast pointer that move forward 2 steps each time
1.3) If the slow pointer and fast pointer both point to the same location after several moving steps, there is a cycle;
1.4) Otherwise, if (fast->next == NULL || fast->next->next == NULL), there has no cycle.
Step 2: If there is a cycle, return the entry location of the cycle
2.1) L1 is defined as the distance between the head point and entry point
2.2) L2 is defined as the distance between the entry point and the meeting point
2.3) C is defined as the length of the cycle
2.4) n is defined as the travel times of the fast pointer around the cycle When the first encounter of the slow pointer and the fast pointer
According to the definition of L1, L2 and C, we can obtain:
the total distance of the slow pointer traveled when encounter is L1 + L2
the total distance of the fast pointer traveled when encounter is L1 + L2 + n * C
Because the total distance the fast pointer traveled is twice as the slow pointer, Thus:
2 (L1+L2) = L1 + L2 + n C => L1 + L2 = n C => L1 = (n - 1) C + (C - L2)
It can be concluded that the distance between the head location and entry location is equal to the distance between the meeting location and the entry location along the direction of forward movement.
So, when the slow pointer and the fast pointer encounter in the cycle, we can define a pointer “entry” that point to the head, this “entry” pointer moves one step each time so as the slow pointer. When this “entry” pointer and the slow pointer both point to the same location, this location is the node where the cycle begins.
================================================================
Here is the code:
|
|
https://leetcode.com/problems/find-the-duplicate-number/description/
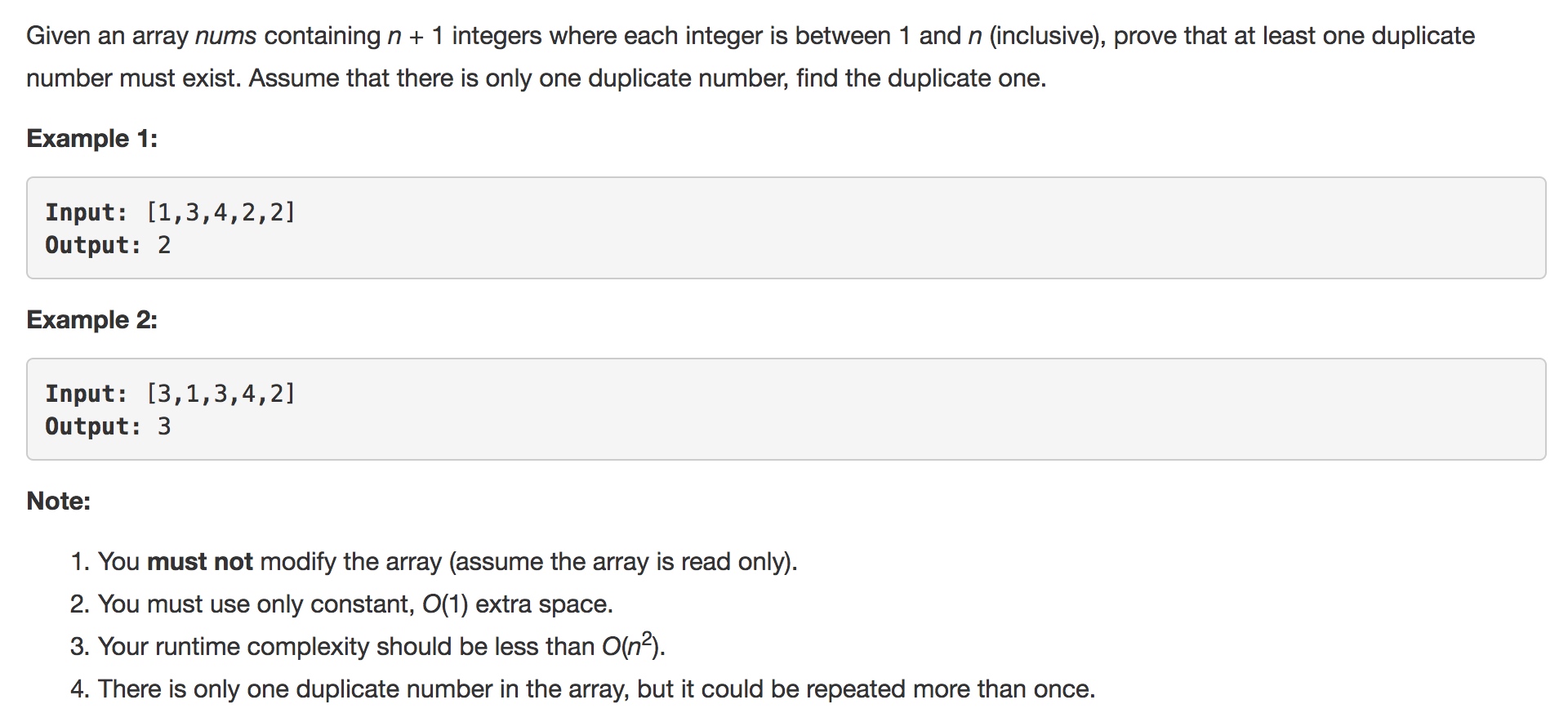
一时没有想出解决办法..
遍历然后二分查找嘛?不可行啊,乱序的
好像xor有用,相同的数xor之后是0,重复次数不定,好像也不好用
题目中强调了1-n,n+1个数,是不是可以利用?
如果分治的话,一侧相同的,左右存在相同的,关键是怎么判断啊
不成,sort,nlogn,然后遍历?好傻,题目规定不能动数组
Cycle detection
可以把问题归约到检测环的问题上!
题目中强调了1 - n, n + 1个数,意思是数在数组的下标范围内。按照下标进行搜寻,如果有重复的值,便会出现环。
检测环的方法,有多种,参见:https://en.wikipedia.org/wiki/Cycle_detection
Floyd’s Tortoise and Hare
思想大致是这样的:让龟兔从同一起点出发,但以不同的速度前进,如果路径没有环的话,那么当兔子走到尽头,龟兔是不会相遇的,如果相遇了,说明成环。
所以这道题,用这样的方式就可以了~
不过,判断除了相交的位置,并不能知道重复的在哪里。
不过,这里不作过多的讨论,有另外的典型题目来讨论这个问题:https://leetcode.com/problems/linked-list-cycle-ii/discuss/44781/Concise-O(n)-solution-by-using-C++-with-Detailed-Alogrithm-Description
|
|
第一个循环,找到了相遇的点,第二个循环利用了起点走到环起点=相遇点走到环起点这一特性:
It can be concluded that the distance between the head location and entry location is equal to the distance between the meeting location and the entry location along the direction of forward movement.