图算法整理（一）：最短路径

Posted on | Edited on | In |

unweighted graph - BFS

BFS即可

1
2
3
4
5
6
7
startNode.dist = 0
enqueue(startNode)
while queue is not empty:
    N = dequeue()
    for each A adjacent N:
        A.dist = N.dist + 1
        enqueue(A)

如书上例图：

从v3出发的BFS最短路径表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int main() {
    size_t V = 7;
    vector<vector<int>> graph(V + 1, vector<int>(V + 1, 0));
    graph[1][2] = 1;
    graph[1][4] = 1;
    graph[2][4] = 1;
    graph[2][5] = 1;
    graph[3][1] = 1;
    graph[3][6] = 1;
    graph[4][3] = 1;
    graph[4][5] = 1;
    graph[4][6] = 1;
    graph[4][7] = 1;
    graph[5][7] = 1;
    graph[7][6] = 1;
    vector<int> dist(V + 1, INT_MAX);
    dist[3] = 0;
    queue<int> q;
    q.push(3);
    while (!q.empty()) {
        int v = q.front();
        q.pop();
        for (int i = 1; i < graph[v].size(); i++) {
            if (graph[v][i] > 0 && dist[i] == INT_MAX) {
                dist[i] = dist[v] + 1;
                q.push(i);
            }
        }
    }
    for (int i = 1; i <= V; i++) {
        cout << dist[i] << " ";
    }
    return 0;
}

输出：

1
1 2 0 2 3 1 3

Dijkstra Shortest Path Algorithm

Greedy Algorithm

始终找最小的，这样保证不用look back:

1
2
3
4
5
6
for i from 1 to n:
    V = min dist unknown vertex
    V.known = true
    for each W adjacent V:
        if W.known == false and W.dist > V.dist + weight(V,W):
            W.dist = V.dist + weight(V,W)

复杂度：

对于基于顶点集 $Q$的实现，算法的运行时间是 $O(|E|\cdot dk{Q}+|V|\cdot em{Q})$，其中 $dk{Q}$和 $em{Q}$分别表示完成键的降序排列时间和从$Q$中提取最小键值的时间。

Dijkstra算法最简单的实现方法是用一个链表或者数组来存储所有顶点的集合$Q$，所以搜索$Q$中最小元素的运算Extract-Min($Q$)只需要线性搜索$Q$中的所有元素。这样的话算法的运行时间是$O(n^{2})$。

对于边数少于$n^{2}$的稀疏图来说，我们可以用邻接表来更有效的实现该算法。同时需要将一个二叉堆或者斐波纳契堆用作优先队列来查找最小的顶点（Extract-Min）。当用到二叉堆的时候，算法所需的时间为 $ {\displaystyle O((m+n)logn)}$，斐波纳契堆能稍微提高一些性能，让算法运行时间达到 ${\displaystyle O(m+nlogn)}$ 。然而，使用斐波纳契堆进行编程，常常会由于算法常数过大而导致速度没有显著提高。

  • 遍历：$O(V^2)$
  • 二叉堆：$O((E + V)logV)$
  • 斐波那契堆：$O(E + VlogV)$

但是，不适用于有负边的：

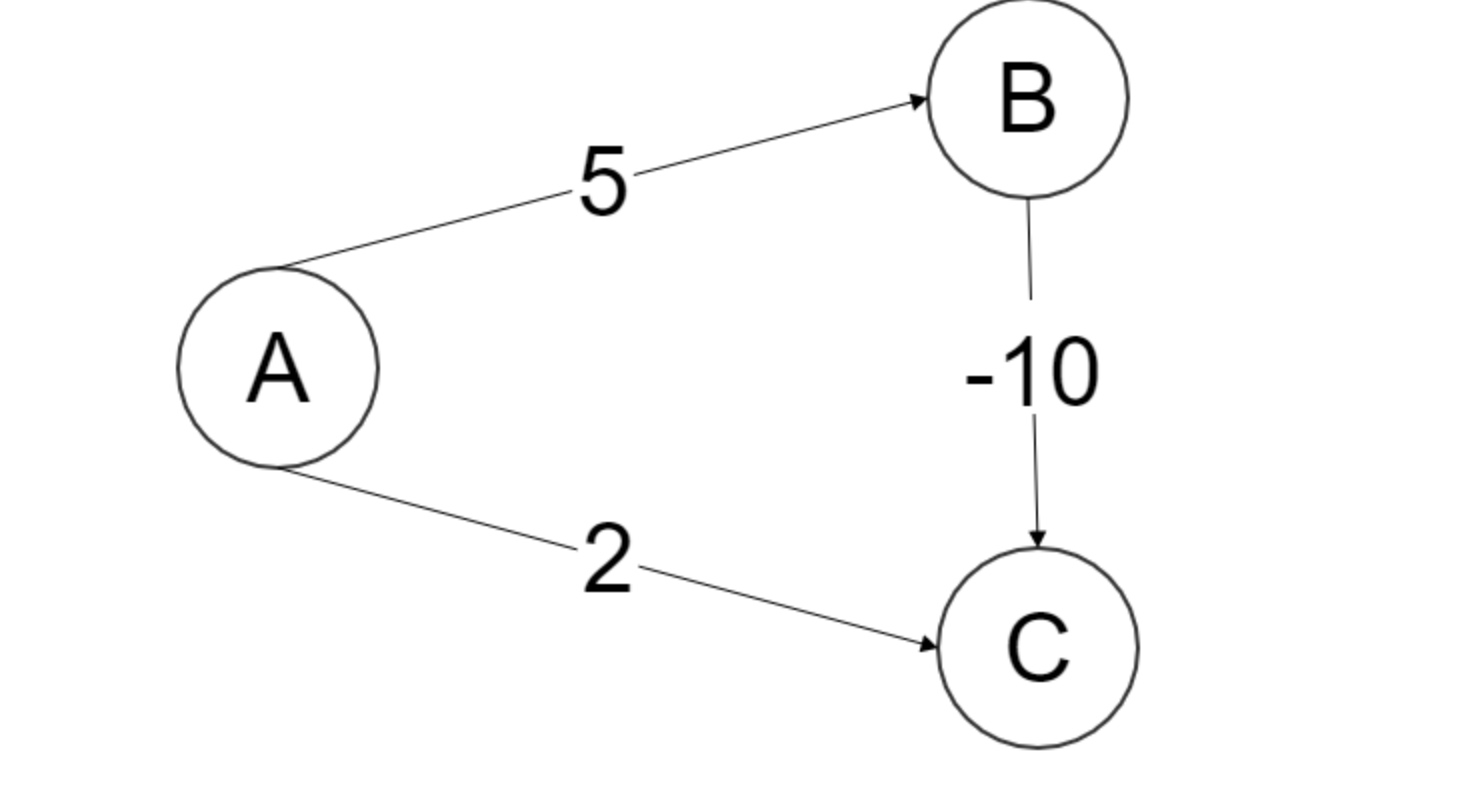
这种情况下，从A出发Dijstra会认为A->C最短为2而不是-5.

实现

书上的示例：

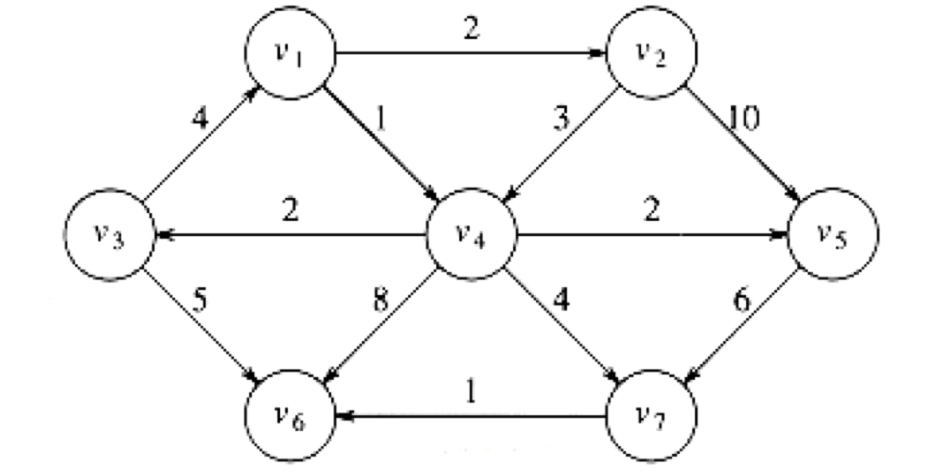
从v1出发：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
//
// Created by Zhao Xiaodong on 2018/4/17.
//
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int main() {
    size_t V = 7;
    vector<vector<int>> graph(V + 1, vector<int>(V + 1, 0));
    graph[1][2] = 2;
    graph[1][4] = 1;
    graph[2][4] = 3;
    graph[2][5] = 10;
    graph[3][1] = 4;
    graph[3][6] = 5;
    graph[4][3] = 2;
    graph[4][5] = 2;
    graph[4][6] = 8;
    graph[4][7] = 4;
    graph[5][7] = 6;
    graph[7][6] = 1;
    vector<int> dist(V + 1, INT_MAX);
    vector<bool> known(V + 1, false);
    vector<int> prev(V + 1, 0);
    dist[1] = 0;
    for (int i = 0; i < V; i++) {
        int minD = INT_MAX;
        int minV = -1;
        for (int j = 1; j <= V; j++) {
            if (!known[j] && minD > dist[j])
                minD = dist[j];
                minV = j;
        }
        known[minV] = true;
        for (int k = 1; k <= graph[minV].size(); ++k) {
            if (graph[minV][k] > 0 && !known[k] && dist[k] > dist[minV] + graph[minV][k]) {
                dist[k] = dist[minV] + graph[minV][k];
                prev[k] = minV;
            }
        }
    }
    for (int i = 1; i <= V; i++) {
        cout << dist[i] << " ";
    }
    return 0;
}

输出:

1
0 2 3 1 3 6 5

Bellman–Ford algorithm

适用于有负边的，但较慢

1
2
3
4
5
6
7
8
9
queue q
while q is not empty:
    v = dequeue(q)
    for each w adjacent v:
        if w.dist > v.dist + cost(v,w):
            w.dist = v.dist + cost(v,w)
            w.path = v
            if w is not in q:
                enqueue(w, q)

复杂度：

时间复杂度：$O(VE)$

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int main() {
    size_t V = 7;
    vector<vector<int>> graph(V + 1, vector<int>(V + 1, 0));
    graph[1][2] = 2;
    graph[1][4] = 1;
    graph[2][4] = 3;
    graph[2][5] = 10;
    graph[3][1] = 4;
    graph[3][6] = 5;
    graph[4][3] = 2;
    graph[4][5] = 2;
    graph[4][6] = 8;
    graph[4][7] = 4;
    graph[5][7] = 6;
    graph[7][6] = 1;
    vector<int> dist(V + 1, INT_MAX);
    vector<int> prev(V + 1, 0);
    dist[1] = 0;
    vector<bool> isInque(V + 1, false);
    queue<int> q;
    q.push(1);
    isInque[1] = true;
    while (!q.empty()) {
        int v = q.front();
        q.pop();
        isInque[v] = false;
        for (int i = 1; i <= V; i++) {
            if (graph[v][i] > 0 && dist[i] > dist[v] + graph[v][i]) {
                dist[i] = dist[v] + graph[v][i];
                prev[i] = v;
                if (!isInque[i])
                    q.push(i);
            }
        }
    }
    for (int i = 1; i <= V; i++) {
        cout << dist[i] << " ";
    }
    return 0;
}

输出：

1
0 2 3 1 3 6 5

All-pair Shortest Path

基本思想

动态规划。

D_k,i,j: 从i到j，只用v_1到v_k做中继节点

意思就是说：从i到j，加入一个中间节点v_k，如果路径里加了这个节点之后，使路径变短，那就更新路径！

pseudocode：

1
2
3
4
5
6
7
8
for i, j:
    D[i][j] = hasEdge(i, j) ? weight[i][j] : inf
for k 1..N:
    for i 1..N:
        for j 1..N:
            if D[i][k] + D[k][j] < D[i][j]:
                D[i][j] = D[i][k] + D[k][j]

伪代码很清楚，中间也没有什么trick，就不实现了

复杂度

复杂度伪代码也表现的很清楚，三层循环，O( N^3 )