图算法整理（四）：最小生成树

Posted on | In |

所有的基础算法，还是要自己再过一遍才放心。

最小生成树的算法过程，既然是最小，自然是一个贪心的过程。

首先明确的一个性质：最小生成树中，边数 = 点数-1

所以，边数是固定的，算法要做的事，找到合法范围内，权值最小的边。

Prim Algorithm

基本思想

跟Dijkstra很像，维护是否确定known，同时不断更新未知点与已知点集的最短距离，选择距离最短的，加入到已知点集中。

pseudocode:

1
2
3
4
5
6
7
8
9
10
for i in [0, V):
    known[i] = false
    dist[i] = inf
dist[x] = 0
for i in [0, V):
    curr = min dist unkonwn vertex
    known[curr] = true
    for each unknown vertex k:
        if hasEdge(curr, k) && dist[curr] + weight(curr, k) < dist[k]:
            dist[k] = dist[curr] + weight(curr, k)

CPP实现

用的示例是书本上的：

-w700

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
//
// Created by Zhao Xiaodong on 2018/8/26.
//
#include <queue>
#include <climits>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
struct Node {
    int k;
    vector<Node *> children;
    Node(int key) : k(key) {}
};
void createNode(int i, vector<int> &parent, vector<Node *> &nodeP) {
    if (nodeP[i])
        return;
    nodeP[i] = new Node(i);
    if (parent[i] != -1) {
        if (!nodeP[parent[i]])
            createNode(parent[i], parent, nodeP);
        nodeP[parent[i]]->children.push_back(nodeP[i]);
    }
}
Node *constructTree(vector<int> &parent) {
    vector<Node *> nodeP(parent.size(), nullptr);
    for (int i = 0; i < parent.size(); i++) {
        createNode(i, parent, nodeP);
    }
    Node *root = nullptr;
    for (int i = 0; i < parent.size(); i++) {
        if (parent[i] == -1)
            root = nodeP[i];
    }
    return root;
}
void levelPrint(Node *root) {
    if (!root)
        cout << "NULL";
    else {
        queue<Node *> q;
        Node *marker = nullptr;
        q.push(root);
        q.push(marker);
        while (!q.empty()) {
            while (q.front()) {
                Node *node = q.front();
                q.pop();
                cout << node->k << " ";
                for (auto child : node->children)
                    q.push(child);
            }
            cout << "\n";
            q.pop();
            if (!q.empty())
                q.push(marker);
        }
    }
}
/////////////////////
void primMST(vector<vector<int>> &g, vector<int> &parent) {
    vector<bool> known(g.size(), false);
    vector<int> dist(g.size(), INT_MAX);
    dist[0] = 0;
    for (int i = 0; i < g.size(); i++) {
        int minD = INT_MAX;
        int curr = -1;
        for (int j = 0; j < g.size(); j++) {
            if (!known[j] && dist[j] < minD) {
                minD = dist[j];
                curr = j;
            }
        }
        known[curr] = true;
        for (int k = 0; k < g.size(); k++) {
            if (!known[k] && g[curr][k] != 0 && g[curr][k] < dist[k]) {
                dist[k] = g[curr][k]; // 更新距离
                parent[k] = curr;
            }
        }
    }
}
/////////////////////
int main() {
    int N = 7;
    vector<vector<int>> g = {
            {0, 2,  4, 1, 0,  0, 0},
            {2, 0,  0, 3, 10, 0, 0},
            {4, 0,  0, 2, 0,  5, 0},
            {1, 3,  2, 0, 7,  8, 4},
            {0, 10, 0, 7, 0,  0, 6},
            {0, 0,  5, 8, 0,  0, 1},
            {0, 0,  0, 4, 6,  1, 0}
    };
    vector<int> parent(N, -1);
    primMST(g, parent);
    Node *root = constructTree(parent);
    levelPrint(root);
    return 0;
}

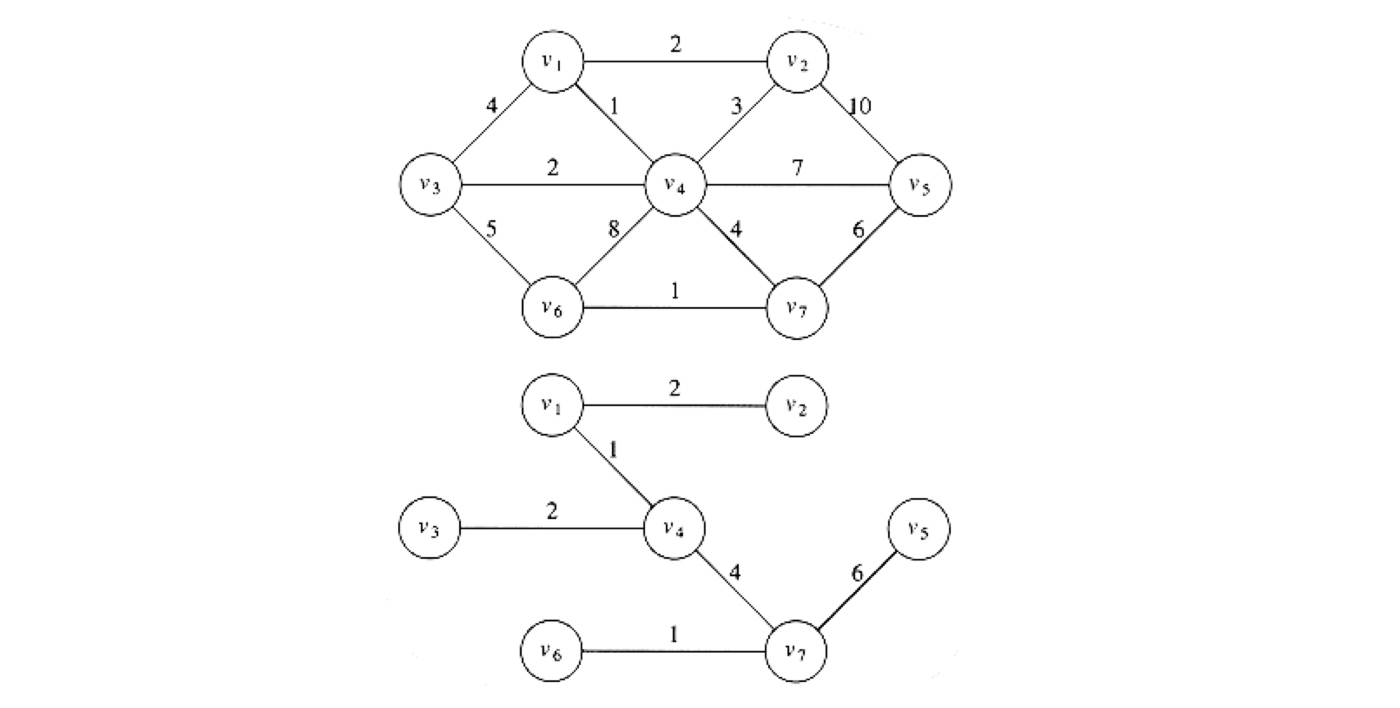
复杂度

时间复杂度：O( N^2 )

适合边稠密的图，跟稠密程度无关

Kruskal Algorithm

基本思想

不是从点出发，不断加入新的点，而是从边的角度看，不断加入新的合法的weight最小的边

边用堆来维护，这样可以每次取出最小的边
同一颗树内的节点，用并查集来维护，方便判断两个点是不是在一棵树内

从零散的N各点，也就是N棵树出发，找到最小的边，如果边所在的两个点不在一棵树，那么加入这条边，然后合并这两个点集；否则这条边不应该出现在最终的生成树种

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
//
// Created by Zhao Xiaodong on 2018/8/26.
//
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> setInit(int size) {
    return vector<int>(size, -1);
}
int setFind(vector<int> &s, int k) {
    if (s[k] < 0)
        return k;
    return s[k] = setFind(s, s[k]);
}
void setUnion(vector<int> &s, int a, int b) {
    int ra = setFind(s, a);
    int rb = setFind(s, b);
    if (ra == rb)
        return;
    if (s[ra] <= s[rb]) {
        s[ra] += s[rb];
        s[rb] = ra;
    } else {
        s[rb] += s[ra];
        s[ra] = rb;
    }
}
int main() {
    int N = 7;
    vector<vector<int>> edges = {
            {0, 1, 2},
            {0, 2, 4},
            {0, 3, 1},
            {1, 3, 3},
            {1, 4, 10},
            {2, 3, 2},
            {2, 5, 5},
            {3, 4, 7},
            {3, 5, 8},
            {3, 6, 4},
            {4, 6, 6},
            {5, 6, 1}
    };
    auto cmp = [](vector<int> &a, vector<int> &b) {
        return a[2] > b[2];
    };
    make_heap(edges.begin(), edges.end(), cmp);
    vector<int> vertSet = setInit(N);
    vector<vector<int>> resEdges;
    int addedEdge = 0;
    while (addedEdge < N - 1) {
        pop_heap(edges.begin(), edges.end(), cmp);
        vector<int> e = edges.back();
        edges.pop_back();
        auto ra = setFind(vertSet, e[0]);
        auto rb = setFind(vertSet, e[1]);
        if (ra != rb) {
            setUnion(vertSet, ra, rb);
            resEdges.push_back(e);
            addedEdge++;
        }
    }
    for (auto &e : resEdges) {
        cout << e[0] << "->" << e[1] << "\n";
    }
    return 0;
}

注意CPP标准库中的堆的使用！

复杂度

E次堆的删除操作，O(ElogE)

适合边稀少的图