Posted on | In , |

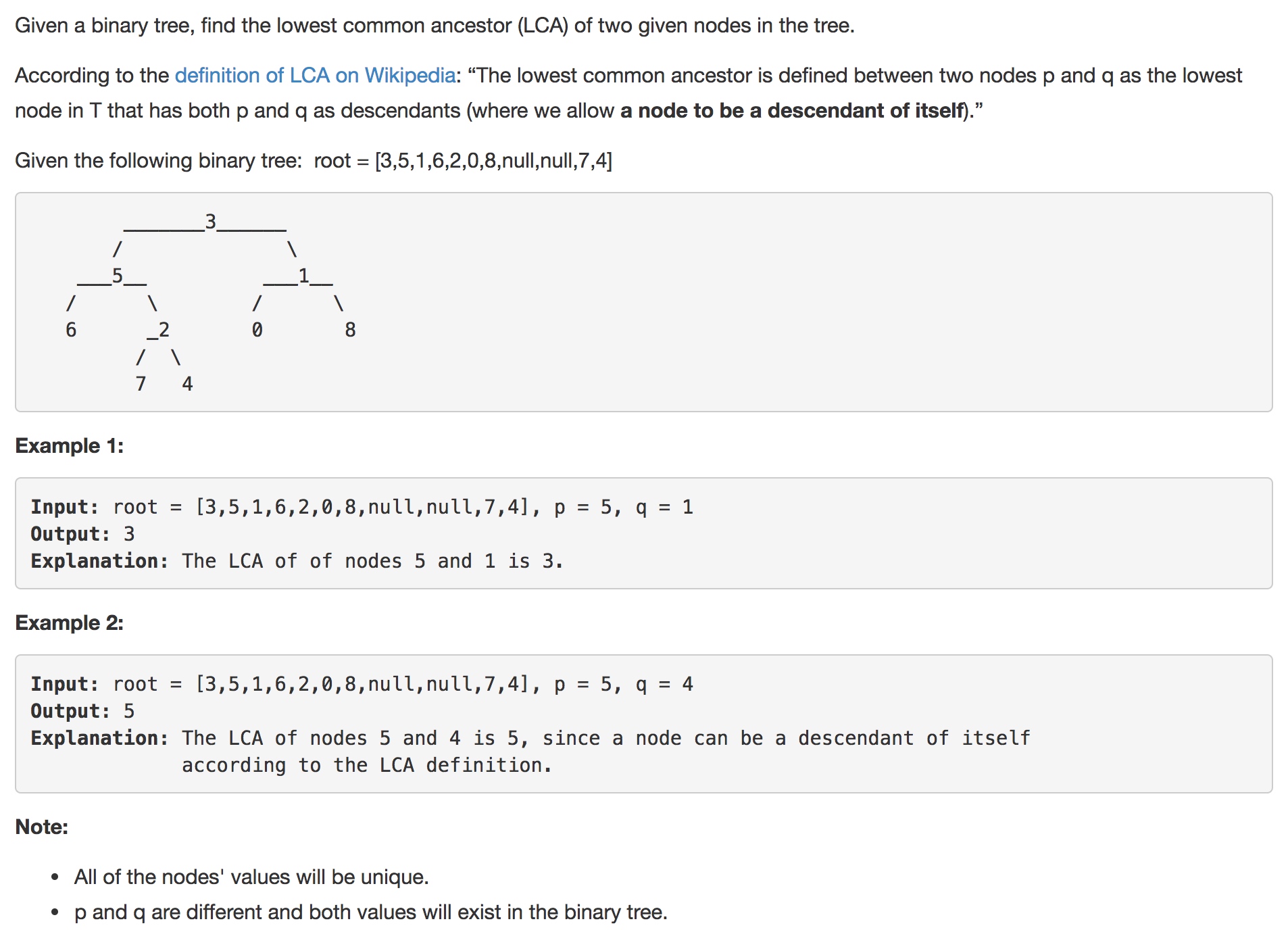
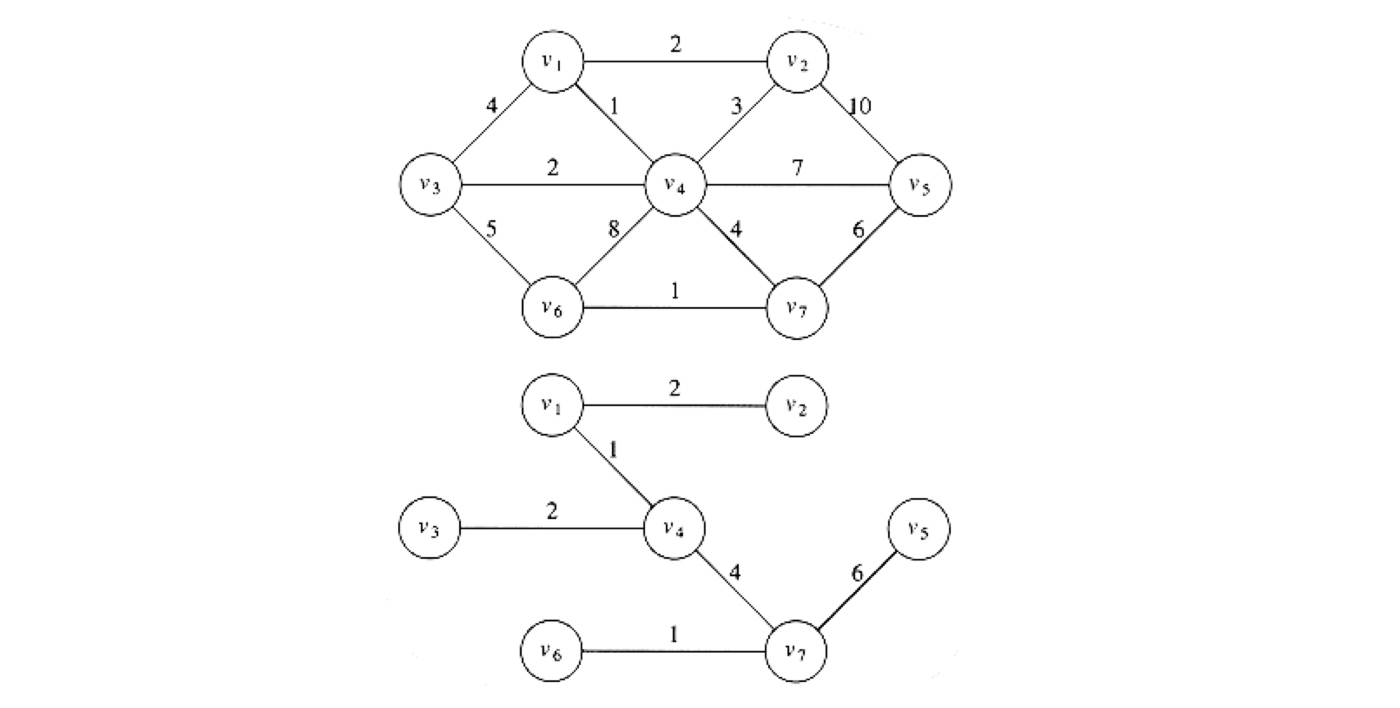
题目

https://leetcode.com/problems/3sum/description/

-w957

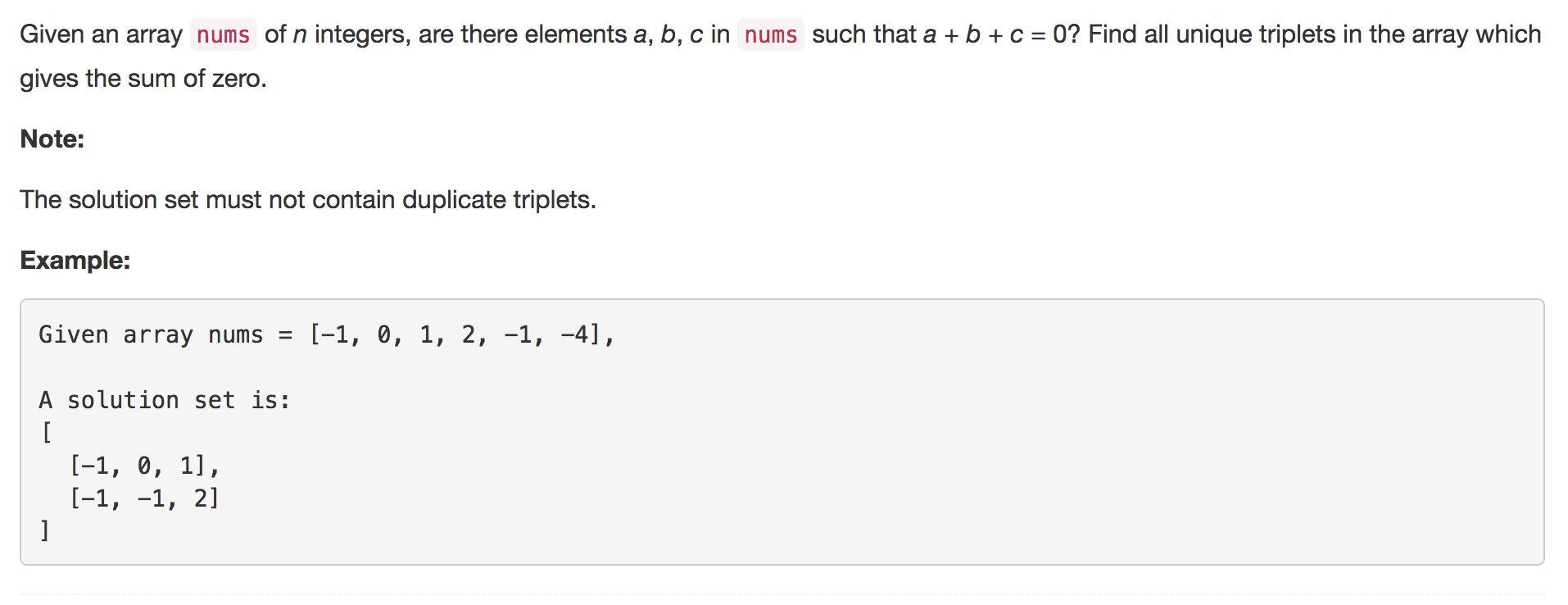
想法

可以说是很经典了。

最naive的方式，三层循环，遍历，O( n^3 ), 肯定不行

先排序，超过了就break，能省一点时间

唉，还有重复的问题呢，答案不能重复

哎呀，不想了，直接看答案吧，这种问题，肯定是那种知道解法之后，终身不忘的

O( N^2 )的解法：

排序
从左往右遍历，确定第一个数A[i]
对于第二个数和第三个数，分别是A[i + 1]和A[n - 1]，一头一尾
如果相加为0，输出
如果大了，右边的往左走，否则，左边往右走

关于重复问题需要判断一下，需要判断一下，找到下一个不重复的

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> res;
        for (int i = 0; i + 2 < nums.size(); i++) {
            if (i > 0 && nums[i] == nums[i - 1])
                continue;
            int a = nums[i];
            int l = i + 1;
            int r = nums.size() - 1;
            while (l < r) {
                if (a + nums[l] + nums[r] < 0) {
                    l++;
                } else if (a + nums[l] + nums[r] > 0) {
                    r--;
                } else {
                    res.push_back({a, nums[l], nums[r]});
                    l++;
                    r--;
                    while (nums[l - 1] == nums[l])
                        l++;
                    while (nums[r + 1] == nums[r])
                        r--;
                }
            }
        }
        return res;
    }
};

这里，重复的判断，就是遇到重复的，就继续向前走，直到不重复！

Posted on | In , |

题目

https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/description/

-w953

想法

自己想的是，dfs找到两者的路径，然后比较两者相同的前缀。

不过，看了discussion中的一个解答之后，发现自己还真是naive了，看准情况，暴力的才是最好的！

答案

我的答案：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    map<int, vector<TreeNode*>> path;
    vector<TreeNode*> curr;
    void dfs(TreeNode* node, int k) {
        if (!node)
            return;
        curr.push_back(node);
        if (node->val == k) {
            path[k] = curr;
        } else {
            dfs(node->left, k);
            dfs(node->right, k);
        }
        curr.pop_back();
    }
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        dfs(root, p->val);
        dfs(root, q->val);
        TreeNode* res = root;
        int i = 0;
        while (true) {
            if (i >= path[p->val].size() || i >= path[q->val].size() || path[p->val][i] != path[q->val][i]) {
                break;
            } else {
                res = path[p->val][i];
                i++;
            }
        }
        return res;
    }
};

discussion中某位的答案：
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/discuss/65225/4-lines-C++JavaPythonRuby

1
2
3
4
5
6
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if (!root || root == p || root == q) return root;
    TreeNode* left = lowestCommonAncestor(root->left, p, q);
    TreeNode* right = lowestCommonAncestor(root->right, p, q);
    return !left ? right : !right ? left : root;
}

Posted on | In , |

题目

1033 To Fill or Not to Fill（25 分）
With highways available, driving a car from Hangzhou to any other city is easy. But since the tank capacity of a car is limited, we have to find gas stations on the way from time to time. Different gas station may give different price. You are asked to carefully design the cheapest route to go.

Input Specification:
Each input file contains one test case. For each case, the first line contains 4 positive numbers: Cmax(≤ 100), the maximum capacity of the tank; D (≤30000), the distance between Hangzhou and the destination city; Davg(≤20), the average distance per unit gas that the car can run; and N (≤ 500), the total number of gas stations. Then N lines follow, each contains a pair of non-negative numbers: P_i, the unit gas price, and D_i(≤D), the distance between this station and Hangzhou, for i=1,⋯,N. All the numbers in a line are separated by a space.

Output Specification:
For each test case, print the cheapest price in a line, accurate up to 2 decimal places. It is assumed that the tank is empty at the beginning. If it is impossible to reach the destination, print The maximum travel distance = X where X is the maximum possible distance the car can run, accurate up to 2 decimal places.

Sample Input 1:

1
2
3
4
5
6
7
8
9
50 1300 12 8
6.00 1250
7.00 600
7.00 150
7.10 0
7.20 200
7.50 400
7.30 1000
6.85 300

Sample Output 1:

1
749.17

Sample Input 2:

1
2
3
50 1300 12 2
7.10 0
7.00 600

Sample Output 2:

1
The maximum travel distance = 1200.00

想法

DP或者贪心吧

找最便宜的GS，然后走最远的路，直到将整个路线覆盖完
实现起来，好像并不是那么容易

不就是遍历嘛，不会太久的hhh

答案

还好AC了，很担心超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
//
// Created by Zhao Xiaodong on 2018/8/27.
//
#include <iostream>
#include <algorithm>
#include <climits>
#include <vector>
using namespace std;
struct Info {
    int distance;
    double price;
};
int main() {
    int CMAX, D, Davg, N;
    cin >> CMAX >> D >> Davg >> N;
    vector<Info> gs(N);
    for (int i = 0; i < N; i++) {
        cin >> gs[i].price >> gs[i].distance;
    }
    auto cmp = [](Info &a, Info &b) {
        return a.price < b.price;
    };
    sort(gs.begin(), gs.end(), cmp);
    vector<bool> road(D, false);
    double cost = 0;
    for (int i = 0; i < gs.size(); i++) {
        if (find(road.begin(), road.end(), false) == road.end())
            break;
        int pos = gs[i].distance;
        int cnt = 0;
        for (int j = pos; j < pos + Davg * CMAX && j < road.size(); j++) {
            if (!road[j]) {
                road[j] = true;
                cnt++;
            }
        }
        cost += cnt * gs[i].price / Davg;
    }
    if (find(road.begin(), road.end(), false) == road.end()) {
        printf("%.2f", cost);
    } else {
        double maxDist = (double) distance(road.begin(), find(road.begin(), road.end(), false));
        printf("The maximum travel distance = %.2f", maxDist);
    }
    return 0;
}

Posted on | In |

有些情况下，一棵树用节点的父节点信息来表示，而很多算法都需要从根出发，去访问节点，于是乎需要前者向后者的转换。

不过，这种算法，估计就是那种很经典，看过就不会忘的，就直接参考网上的了：
https://www.geeksforgeeks.org/construct-a-binary-tree-from-parent-array-representation/

基本思想

记录每个节点的指针：nodeP

当节点尚未生成，即nodeP还为null，生成一个节点，将其父节点指针对应孩子指向它，如果此时父节点并未生成，那么递归的生成

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
//
// Created by Zhao Xiaodong on 2018/8/26.
//
#include <vector>
#include <queue>
#include <iostream>
#include <climits>
using namespace std;
struct Node {
    int k;
    vector<Node *> children;
    Node(int key) : k(key) {}
};
void createNode(int i, vector<int> &parent, vector<Node *>& nodeP) {
    if (nodeP[i])
        return;
    nodeP[i] = new Node(i);
    if (parent[i] != -1) {
        if (!nodeP[parent[i]])
            createNode(parent[i], parent, nodeP);
        nodeP[parent[i]]->children.push_back(nodeP[i]);
    }
}
Node *constructTree(vector<int> &parent) {
    vector<Node *> nodeP(parent.size(), nullptr);
    for (int i = 0; i < parent.size(); i++) {
        createNode(i, parent, nodeP);
    }
    Node *root = nullptr;
    for (int i = 0; i < parent.size(); i++) {
        if (parent[i] == -1)
            root = nodeP[i];
    }
    return root;
}
void levelPrint(Node *root) {
    if (!root)
        cout << "NULL";
    else {
        queue<Node *> q;
        Node *marker = nullptr;
        q.push(root);
        q.push(marker);
        while (!q.empty()) {
            while (q.front()) {
                Node *node = q.front();
                q.pop();
                cout << node->k << " ";
                for (auto child : node->children)
                    q.push(child);
            }
            cout << "\n";
            q.pop();
            if (!q.empty())
                q.push(marker);
        }
    }
}
int main() {
    vector<int> parent = {-1, 0, 3, 0, 6, 6, 3};
    Node *root = constructTree(parent);
    levelPrint(root);
    return 0;
}

复杂度分析

时间

每调用一次createNode生成一个节点，而createNode中没有什么循环之类的操作，所以，时间复杂度O(N)

空间

需要一个nodeP数组，所以空间复杂度是O(N)

Posted on | In |

所有的基础算法，还是要自己再过一遍才放心。

最小生成树的算法过程，既然是最小，自然是一个贪心的过程。

首先明确的一个性质：最小生成树中，边数 = 点数-1

所以，边数是固定的，算法要做的事，找到合法范围内，权值最小的边。

Prim Algorithm

基本思想

跟Dijkstra很像，维护是否确定known，同时不断更新未知点与已知点集的最短距离，选择距离最短的，加入到已知点集中。

pseudocode:

1
2
3
4
5
6
7
8
9
10
for i in [0, V):
    known[i] = false
    dist[i] = inf
dist[x] = 0
for i in [0, V):
    curr = min dist unkonwn vertex
    known[curr] = true
    for each unknown vertex k:
        if hasEdge(curr, k) && dist[curr] + weight(curr, k) < dist[k]:
            dist[k] = dist[curr] + weight(curr, k)

CPP实现

用的示例是书本上的：

-w700

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
//
// Created by Zhao Xiaodong on 2018/8/26.
//
#include <queue>
#include <climits>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
struct Node {
    int k;
    vector<Node *> children;
    Node(int key) : k(key) {}
};
void createNode(int i, vector<int> &parent, vector<Node *> &nodeP) {
    if (nodeP[i])
        return;
    nodeP[i] = new Node(i);
    if (parent[i] != -1) {
        if (!nodeP[parent[i]])
            createNode(parent[i], parent, nodeP);
        nodeP[parent[i]]->children.push_back(nodeP[i]);
    }
}
Node *constructTree(vector<int> &parent) {
    vector<Node *> nodeP(parent.size(), nullptr);
    for (int i = 0; i < parent.size(); i++) {
        createNode(i, parent, nodeP);
    }
    Node *root = nullptr;
    for (int i = 0; i < parent.size(); i++) {
        if (parent[i] == -1)
            root = nodeP[i];
    }
    return root;
}
void levelPrint(Node *root) {
    if (!root)
        cout << "NULL";
    else {
        queue<Node *> q;
        Node *marker = nullptr;
        q.push(root);
        q.push(marker);
        while (!q.empty()) {
            while (q.front()) {
                Node *node = q.front();
                q.pop();
                cout << node->k << " ";
                for (auto child : node->children)
                    q.push(child);
            }
            cout << "\n";
            q.pop();
            if (!q.empty())
                q.push(marker);
        }
    }
}
/////////////////////
void primMST(vector<vector<int>> &g, vector<int> &parent) {
    vector<bool> known(g.size(), false);
    vector<int> dist(g.size(), INT_MAX);
    dist[0] = 0;
    for (int i = 0; i < g.size(); i++) {
        int minD = INT_MAX;
        int curr = -1;
        for (int j = 0; j < g.size(); j++) {
            if (!known[j] && dist[j] < minD) {
                minD = dist[j];
                curr = j;
            }
        }
        known[curr] = true;
        for (int k = 0; k < g.size(); k++) {
            if (!known[k] && g[curr][k] != 0 && g[curr][k] < dist[k]) {
                dist[k] = g[curr][k]; // 更新距离
                parent[k] = curr;
            }
        }
    }
}
/////////////////////
int main() {
    int N = 7;
    vector<vector<int>> g = {
            {0, 2,  4, 1, 0,  0, 0},
            {2, 0,  0, 3, 10, 0, 0},
            {4, 0,  0, 2, 0,  5, 0},
            {1, 3,  2, 0, 7,  8, 4},
            {0, 10, 0, 7, 0,  0, 6},
            {0, 0,  5, 8, 0,  0, 1},
            {0, 0,  0, 4, 6,  1, 0}
    };
    vector<int> parent(N, -1);
    primMST(g, parent);
    Node *root = constructTree(parent);
    levelPrint(root);
    return 0;
}

复杂度

时间复杂度：O( N^2 )

适合边稠密的图，跟稠密程度无关

Kruskal Algorithm

基本思想

不是从点出发，不断加入新的点，而是从边的角度看，不断加入新的合法的weight最小的边

边用堆来维护，这样可以每次取出最小的边
同一颗树内的节点，用并查集来维护，方便判断两个点是不是在一棵树内

从零散的N各点，也就是N棵树出发，找到最小的边，如果边所在的两个点不在一棵树，那么加入这条边，然后合并这两个点集；否则这条边不应该出现在最终的生成树种

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
//
// Created by Zhao Xiaodong on 2018/8/26.
//
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> setInit(int size) {
    return vector<int>(size, -1);
}
int setFind(vector<int> &s, int k) {
    if (s[k] < 0)
        return k;
    return s[k] = setFind(s, s[k]);
}
void setUnion(vector<int> &s, int a, int b) {
    int ra = setFind(s, a);
    int rb = setFind(s, b);
    if (ra == rb)
        return;
    if (s[ra] <= s[rb]) {
        s[ra] += s[rb];
        s[rb] = ra;
    } else {
        s[rb] += s[ra];
        s[ra] = rb;
    }
}
int main() {
    int N = 7;
    vector<vector<int>> edges = {
            {0, 1, 2},
            {0, 2, 4},
            {0, 3, 1},
            {1, 3, 3},
            {1, 4, 10},
            {2, 3, 2},
            {2, 5, 5},
            {3, 4, 7},
            {3, 5, 8},
            {3, 6, 4},
            {4, 6, 6},
            {5, 6, 1}
    };
    auto cmp = [](vector<int> &a, vector<int> &b) {
        return a[2] > b[2];
    };
    make_heap(edges.begin(), edges.end(), cmp);
    vector<int> vertSet = setInit(N);
    vector<vector<int>> resEdges;
    int addedEdge = 0;
    while (addedEdge < N - 1) {
        pop_heap(edges.begin(), edges.end(), cmp);
        vector<int> e = edges.back();
        edges.pop_back();
        auto ra = setFind(vertSet, e[0]);
        auto rb = setFind(vertSet, e[1]);
        if (ra != rb) {
            setUnion(vertSet, ra, rb);
            resEdges.push_back(e);
            addedEdge++;
        }
    }
    for (auto &e : resEdges) {
        cout << e[0] << "->" << e[1] << "\n";
    }
    return 0;
}

注意CPP标准库中的堆的使用！

复杂度

E次堆的删除操作，O(ElogE)

适合边稀少的图

Posted on | In , |

题目

https://pintia.cn/problem-sets/994805342720868352/problems/994805396953219072

1072 Gas Station（30 分）
A gas station has to be built at such a location that the minimum distance between the station and any of the residential housing is as far away as possible. However it must guarantee that all the houses are in its service range.

Now given the map of the city and several candidate locations for the gas station, you are supposed to give the best recommendation. If there are more than one solution, output the one with the smallest average distance to all the houses. If such a solution is still not unique, output the one with the smallest index number.

Input Specification:
Each input file contains one test case. For each case, the first line contains 4 positive integers: N ( ≤10^3 ), the total number of houses; M ( ≤10 ), the total number of the candidate locations for the gas stations; K ( ≤10^4 ), the number of roads connecting the houses and the gas stations; and D_S, the maximum service range of the gas station. It is hence assumed that all the houses are numbered from 1 to N, and all the candidate locations are numbered from G1 to GM.

Then K lines follow, each describes a road in the format

1
P1 P2 Dist

where P1 and P2 are the two ends of a road which can be either house numbers or gas station numbers, and Dist is the integer length of the road.

Output Specification:
For each test case, print in the first line the index number of the best location. In the next line, print the minimum and the average distances between the solution and all the houses. The numbers in a line must be separated by a space and be accurate up to 1 decimal place. If the solution does not exist, simply output No Solution.

Sample Input 1:

1
2
3
4
5
6
7
8
9
10
11
12
4 3 11 5
1 2 2
1 4 2
1 G1 4
1 G2 3
2 3 2
2 G2 1
3 4 2
3 G3 2
4 G1 3
G2 G1 1
G3 G2 2

Sample Output 1:

1
2
G1
2.0 3.3

Sample Input 2:

1
2
3
2 1 2 10
1 G1 9
2 G1 20

Sample Output 2:

1
No Solution

想法

找的距离最近house最远的比较容易

找距离最远的house最近的话，需要遍历

还要计算平均距离，那么肯定要遍历一遍了

又是Dijkstra，加一堆麻烦的东西，唉，这种题要写很久orz

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
//
// Created by Zhao Xiaodong on 2018/8/24.
//
#include <queue>
#include <vector>
#include <algorithm>
#include <iostream>
#include <climits>
using namespace std;
int main() {
    int N, M, K, D;
    scanf("%d %d %d %d", &N, &M, &K, &D);
    vector<vector<int>> g(M + N + 1, vector<int>(M + N + 1, INT_MAX));
    for (int i = 0; i < K; i++) {
        char p1[10];
        char p2[10];
        int dist;
        int pi1, pi2;
        scanf("%s %s %d", &p1, &p2, &dist);
        if (isdigit(p1[0])) {
            pi1 = stoi(p1);
        } else {
            pi1 = stoi(p1 + 1) + N;
        }
        if (isdigit(p2[0])) {
            pi2 = stoi(p2);
        } else {
            pi2 = stoi(p2 + 1) + N;
        }
        g[pi1][pi2] = g[pi2][pi1] = dist;
    }
    int bestGS = -1;
    double maxMinDist = -1.0;
    double minAvgDist = 1000000000;
    for (int gs = N + 1; gs <= N + M; gs++) {
        vector<int> dist(N + M + 1, INT_MAX);
        vector<int> done(N + M + 1, false);
        dist[gs] = 0;
        for (int i = 1; i < N + M + 1; i++) {
            int minD = INT_MAX;
            int curr = 0;
            for (int j = 1; j < N + M + 1; j++) {
                if (!done[j] && dist[j] < minD) {
                    minD = dist[j];
                    curr = j;
                }
            }
            done[curr] = true;
            for (int k = 1; k < N + M + 1; k++) {
                if (g[curr][k] != INT_MAX && dist[curr] + g[curr][k] < dist[k]) {
                    dist[k] = dist[curr] + g[curr][k];
                }
            }
        }
        int totalDist = 0;
        int minDist = INT_MAX;
        bool isValid = true;
        for (int i = 1; i < N + 1; i++) {
            if (dist[i] > D) {
                isValid = false;
                break;
            }
            totalDist += dist[i];
            if (dist[i] < minDist)
                minDist = dist[i];
        }
        if (isValid) {
            if (minDist > maxMinDist) {
                maxMinDist = minDist;
                bestGS = gs - N;
                minAvgDist = 1.0 * totalDist / N;
            } else if (minDist == maxMinDist) {
                if (1.0 * totalDist / N < minAvgDist) {
                    bestGS = gs - N;
                    minAvgDist = 1.0 * totalDist / N;
                }
            }
        }
    }
    if (bestGS != -1) {
        printf("G%d\n", bestGS);
        printf("%.1f %.1f", maxMinDist, minAvgDist);
    } else {
        printf("No Solution");
    }
    return 0;
}

Posted on | In , |

题目

https://pintia.cn/problem-sets/994805342720868352/problems/994805464397627392

1030 Travel Plan (30)（30 分）
A traveler’s map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 4 positive integers N, M, S, and D, where N (<=500) is the number of cities (and hence the cities are numbered from 0 to N-1); M is the number of highways; S and D are the starting and the destination cities, respectively. Then M lines follow, each provides the information of a highway, in the format:

City1 City2 Distance Cost

where the numbers are all integers no more than 500, and are separated by a space.

Output Specification:

For each test case, print in one line the cities along the shortest path from the starting point to the destination, followed by the total distance and the total cost of the path. The numbers must be separated by a space and there must be no extra space at the end of output.

Sample Input

1
2
3
4
5
6
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20

Sample Output

1
0 2 3 3 40

想法

很经典的一道题

Dijkstra，需要记录路径，distance+cost

记下可以时常温习

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
//
// Created by Zhao Xiaodong on 2018/8/24.
//
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int N, M, start, dst;
    cin >> N >> M >> start >> dst;
    vector<vector<int>> g(N, vector<int>(N, INT_MAX));
    vector<vector<int>> cost(N, vector<int>(N, INT_MAX));
    for (int i = 0; i < M; i++) {
        int c1, c2, dist, c;
        cin >> c1 >> c2 >> dist >> c;
        g[c1][c2] = g[c2][c1] = dist;
        cost[c1][c2] = cost[c2][c1] = c;
    }
    vector<bool> done(N, false);
    vector<int> prev(N, -1);
    vector<int> minDist(N, INT_MAX);
    vector<int> minCost(N, INT_MAX);
    minDist[start] = 0;
    minCost[start] = 0;
    while (true) {
        int minD = INT_MAX;
        int curr = 0;
        for (int i = 0; i < N; i++) {
            if (!done[i] && minDist[i] < minD) {
                minD = minDist[i];
                curr = i;
            }
        }
        done[curr] = true;
        if (done[dst])
            break;
        for (int i = 0; i < N; i++) {
            if (g[curr][i] == INT_MAX)
                continue;
            else {
                if (g[curr][i] + minDist[curr] < minDist[i]) {
                    minDist[i] = g[curr][i] + minDist[curr];
                    prev[i] = curr;
                    minCost[i] = minCost[curr] + cost[curr][i];
                } else if (g[curr][i] + minDist[curr] == minDist[i]) {
                    if (minCost[curr] + cost[curr][i] < minCost[i]) {
                        prev[i] = curr;
                        minCost[i] = minCost[curr] + cost[curr][i];
                    }
                }
            }
        }
    }
    vector<int> path;
    for (int p = dst; p != start; p = prev[p]) {
        path.push_back(p);
    }
    path.push_back(start);
    reverse(path.begin(), path.end());
    cout << path[0];
    for (int i = 1; i < path.size(); i++) {
        cout << " " << path[i];
    }
    cout << " " << minDist[dst] << " " << minCost[dst];
    return 0;
}

Posted on | In , |

题目

https://pintia.cn/problem-sets/994805342720868352/problems/994805402305150976

1068 Find More Coins（30 分）

Eva loves to collect coins from all over the universe, including some other planets like Mars. One day she visited a universal shopping mall which could accept all kinds of coins as payments. However, there was a special requirement of the payment: for each bill, she must pay the exact amount. Since she has as many as 10^4 coins with her, she definitely needs your help. You are supposed to tell her, for any given amount of money, whether or not she can find some coins to pay for it.

Input Specification:
Each input file contains one test case. For each case, the first line contains 2 positive numbers: N (≤10^4 , the total number of coins) and M (≤10^2 , the amount of money Eva has to pay). The second line contains N face values of the coins, which are all positive numbers. All the numbers in a line are separated by a space.

Output Specification:
For each test case, print in one line the face values V1 ≤ V​2 ≤ ⋯ ≤ V_k such that V_1 + V_2 + ⋯ + V_k = M. All the numbers must be separated by a space, and there must be no extra space at the end of the line. If such a solution is not unique, output the smallest sequence. If there is no solution, output “No Solution” instead.

Note: sequence {A[1], A[2], …} is said to be “smaller” than sequence {B[1], B[2], …} if there exists k≥1 such that A[i]=B[i] for all i<k, and A[k] < B[k].

Sample Input 1:

1
2
8 9
5 9 8 7 2 3 4 1

Sample Output 1:

1
1 3 5

Sample Input 2:

1
2
4 8
7 2 4 3

Sample Output 2:

1
No Solution

想法

先排序 肯定的

backtracking？感觉是

写了一个递归的版本，超时了一个点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
//
// Created by Zhao Xiaodong on 2018/8/23.
//
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int N, M;
vector<int> s;
vector<int> a;
int sum = 0;
bool f(int k) {
    if (sum == M)
        return true;
    for (int i = k; i < N; i++) {
        s.push_back(a[i]);
        sum += a[i];
        if (sum == M)
            return true;
        else if (sum > M) {
            sum -= a[i];
            s.pop_back();
            return false;
        }
        bool res = f(i + 1);
        if (res) {
            return true;
        }
        sum -= a[i];
        s.pop_back();
    }
    return false;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> N >> M;
    a = vector<int>(N);
    for (int i = 0; i < N; i++) {
        cin >> a[i];
    }
    sort(a.begin(), a.end());
    bool res = f(0);
    if (res) {
        if (!s.empty()) {
            cout << s[0];
            for (int i = 1; i < s.size(); i++) {
                cout << " " << s[i];
            }
            cout << "\n";
        }
    } else {
        cout << "No Solution";
    }
    return 0;
}

有没有可以优化的地方？

TODO..

或许应该用DP吧

Posted on | In , |

题目

https://pintia.cn/problem-sets/994805342720868352/problems/994805403651522560

Given any permutation of the numbers {0, 1, 2,…, N−1}, it is easy to sort them in increasing order. But what if Swap(0, *) is the ONLY operation that is allowed to use? For example, to sort {4, 0, 2, 1, 3} we may apply the swap operations in the following way:

1
2
3
Swap(0, 1) => {4, 1, 2, 0, 3}
Swap(0, 3) => {4, 1, 2, 3, 0}
Swap(0, 4) => {0, 1, 2, 3, 4}

Now you are asked to find the minimum number of swaps need to sort the given permutation of the first N nonnegative integers.

Input Specification:
Each input file contains one test case, which gives a positive N (≤10^5​​) followed by a permutation sequence of {0, 1, …, N−1}. All the numbers in a line are separated by a space.

Output Specification:
For each case, simply print in a line the minimum number of swaps need to sort the given permutation.

Sample Input:

1
2
10
3 5 7 2 6 4 9 0 8 1

Sample Output:

1
9

想法

一眼看过去，应该是一道技巧题，不是常规的数据结构和算法。

每一步，把逆序数降到最低。
好像不止，要把每一个都调整到对应的位置。

唉，那是不是，多少个不在自己位置的，就换多少次对了。

怎么有点连通分量的味道，如果哪几个之间错位了，就需要借助一次0位置进行调整。

如果k个之间错位：
包括0：k-1次；不包括0：k+1次

唉，AC了，果然是trick啊，好好想，细细想，这种题估计就是一个小转弯，工作量并不大

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//
// Created by Zhao Xiaodong on 2018/8/23.
//
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int N;
    cin >> N;
    if (N == 0) {
        cout << 0;
        return 0;
    }
    vector<int> a(N);
    for (int i = 0; i < N; i++) {
        cin >> a[i];
    }
    vector<int> marked(N, false);
    int res = 0;
    if (a[0] != 0) {
        marked[0] = true;
        for (int i = a[0]; i != 0; i = a[i]) {
            marked[i] = true;
            res++;
        }
    }
    for (int i = 1; i < N; i++) {
        if (a[i] != i && !marked[i]) {
            res += 2;
            marked[i] = true;
            for (int j = a[i]; j != i && !marked[j]; j = a[j]) {
                marked[j] = true;
                res++;
            }
        }
    }
    cout << res;
    return 0;
}

Posted on | In , |

题目

https://leetcode.com/problems/sort-list/description/

-w956

想法

归并排序

链表操作比较烦

答案

自己写的一个归并排序，好多地方应该可以优化，不过AC了，就不说什么了：

不过用了递归，这个空间复杂度，恐怕不是O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
private:
    ListNode *mergeSort(ListNode *head, int len) {
        if (len == 1) {
            head->next = NULL;
            return head;
        }
        if (len == 2) {
            if (head->val <= head->next->val) {
                head->next->next = NULL;
                return head;
            } else {
                ListNode *newHead = head->next;
                newHead->next = head;
                newHead->next->next = NULL;
                return newHead;
            }
        }
        int mid = len / 2;
        ListNode *p = head;
        for (int i = 0; i < mid; i++) {
            p = p->next;
        }
        ListNode *headL = mergeSort(head, mid);
        ListNode *headR = mergeSort(p, len - mid);
        ListNode dummy(0);
        p = &dummy;
        while (headL && headR) {
            if (headL->val <= headR->val) {
                p->next = headL;
                headL = headL->next;
            } else {
                p->next = headR;
                headR = headR->next;
            }
            p = p->next;
        }
        while (headL) {
            p->next = headL;
            headL = headL->next;
            p = p->next;
        }
        while (headR) {
            p->next = headR;
            headR = headR->next;
            p = p->next;
        }
        return dummy.next;
    }
public:
    ListNode *sortList(ListNode *head) {
        if (!head)
            return NULL;
        int len = 0;
        ListNode *p = head;
        while (p) {
            len++;
            p = p->next;
        }
        ListNode *ret = mergeSort(head, len);
        return ret;
    }
};